
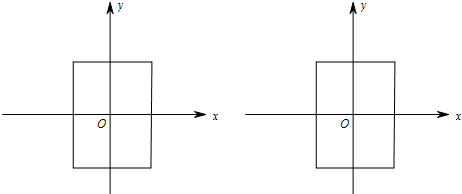
���� ��1���߶�AD��BC�ġ��ܾࡱ��AB��DC�ij��ȣ�
��2�������ֱ��OA�Ľ���ʽ����ֱ֪��EF��OA��ֱ���ʵ�C��ֱ��EF�ľ���Ϊ����ࡱ��
��3������ͼ��K��BD��ʱ���ܾ�����Сֵ����OK��ADʱ���ܾ������ֵ��
�ڵ��ı���KLMNΪ������ʱ��������ֵ��
��� �⣺��1����ͼ��
�ɴ��ߵ����ʿ�֪���߶�AD��BC�ġ��ܾࡱ��AB��DC�ij��ȣ��ʡ��ܾࡱ��6��
��Rt��ADC�У�AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10������ࡱ��10��
��2������ͼ��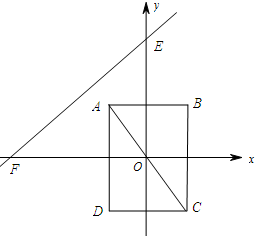
��ֱ��OA�Ľ���ʽΪy=kx��
��x=-3��y=4���뺯���Ľ���ʽ�ã�k=-$\frac{4}{3}$��
��ֱ��EF�Ľ���ʽΪy=$\frac{3}{4}x+b$��
��ֱ��OA��EF���ֱ��
��EF�����ABCD�ġ��ܾࡱ��1��
���C��EF�ľ����=10+1=11��������ࡱ=11��
��3����ͼ��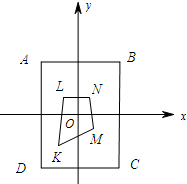
�ٵ�K��BD��ʱ������ABCD���ı���KLMN�ġ���ࡱΪKB=7��
��KD=BD-BK=10-7=3��������ܾ�=3
����ͼ��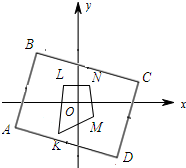
��OK��ADʱ������ABCD���ı���KLMN�ġ��ܾࡱ����Сֵ��
�߾��εĿ�Ϊ6�������ܾ����Сֵ=6��2-2=1��
���ܾ�ķ�ΧΪ��1���ܾ��3��
������ͼ��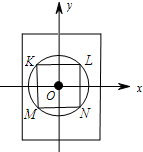
���ı���KLMNΪ�����Σ��Ҹ��㵽ԭ��ľ���Ϊ2ʱ���ı��ε�KLMN��������
S�ı���KLMN=$\frac{1}{2}KN•ML$=$\frac{1}{2}��4��4$=8��
���� ������Ҫ�������һ�κ����������ľ���͵㵽ֱ�ߵľ����Ӧ�ã����ⶨ�壬�������⻭��ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$cm��3��cm2 | B�� | 2$\sqrt{2}$cm��3��cm2 | C�� | 2$\sqrt{2}$cm��6��cm2 | D�� | $\sqrt{10}$cm��6��cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
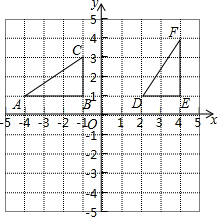 ��ͼ����ABC�͡�DEF��ֱ������ϵ�е�λ����ͼ��ʾ��
��ͼ����ABC�͡�DEF��ֱ������ϵ�е�λ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
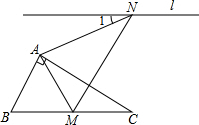 ��ͼ������30���ֱ�����ǰ��ABC����BAC=90�㣬��C=30�㣬����ABC���ŵ�A��ʱ����ת���õ���AMN��ʹ�õ�B����BC���ϵĵ�M��������N��ֱ��l��BC�����1�Ķ���Ϊ��������
��ͼ������30���ֱ�����ǰ��ABC����BAC=90�㣬��C=30�㣬����ABC���ŵ�A��ʱ����ת���õ���AMN��ʹ�õ�B����BC���ϵĵ�M��������N��ֱ��l��BC�����1�Ķ���Ϊ��������| A�� | 15�� | B�� | 30�� | C�� | 45�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
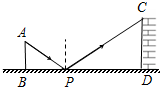 ��ͼ�ǿ���������ֵ�������ij�ų�ǽ�߶ȵ�ʾ��ͼ����P����һˮƽ��ƽ�澵�����ߴӵ�A������ƽ�澵�����պ��䵽�ų�ǽCD�Ķ���C������֪ AB��BD��CD��BD���Ҳ��AB=6�ף�BP=9�ף�PD=15�ף���ô�ùų�ǽ�ĸ߶��ǣ�������
��ͼ�ǿ���������ֵ�������ij�ų�ǽ�߶ȵ�ʾ��ͼ����P����һˮƽ��ƽ�澵�����ߴӵ�A������ƽ�澵�����պ��䵽�ų�ǽCD�Ķ���C������֪ AB��BD��CD��BD���Ҳ��AB=6�ף�BP=9�ף�PD=15�ף���ô�ùų�ǽ�ĸ߶��ǣ�������| A�� | 6�� | B�� | 8�� | C�� | 10�� | D�� | 15�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
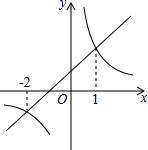 һ�κ���y1=k1x+b�ͷ���������y2=$\frac{{k}_{2}}{x}$��k1k2?��0����ͼ����ͼ��ʾ����y1��y2����x��ȡֵ��Χ��-2��x��0��x��1��
һ�κ���y1=k1x+b�ͷ���������y2=$\frac{{k}_{2}}{x}$��k1k2?��0����ͼ����ͼ��ʾ����y1��y2����x��ȡֵ��Χ��-2��x��0��x��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
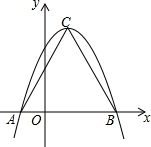 ��ͼ�����κ���y=-x2+2x+3��ͼ����x�ύ�ڵ�A�͵�B������ΪC����sin��ABC=��������
��ͼ�����κ���y=-x2+2x+3��ͼ����x�ύ�ڵ�A�͵�B������ΪC����sin��ABC=��������| A�� | $\frac{2\sqrt{5}}{5}$ | B�� | $\frac{\sqrt{5}}{5}$ | C�� | 2 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
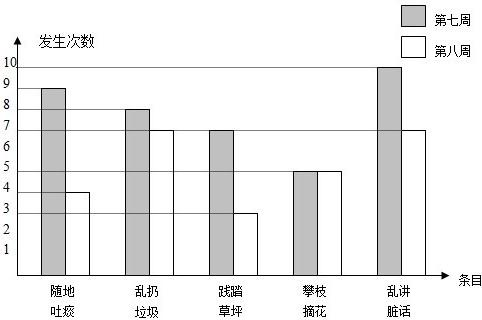
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com