练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．若0.000204用科学记数法可以记为2.04×10n，则n=-4．

    分析 绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

    解答 解：0.000204=2.04×10-4=2.04×10n，
    ∴n=-4，
    故答案为：-4．

    点评 本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

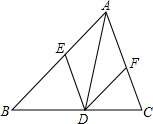    2．如图，已知AD是△ABC的角平分线，点E、F分别是边AC、AB的中点，连接DE、DF，要使四边形AEDF称为菱形，还需添加一个条件，这个条件可以是AB=AC、∠B=∠C或AE=AF（答案不唯一）．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：
    ①BE=$\frac{1}{2}$GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH
    其中，正确的结论有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．不等式组$\left\{\begin{array}{l}{x-3≥0}\\{\frac{1}{2}（x+3）≤1}\end{array}\right.$的解集在数轴上表示正确的是（　　）
    A．B．
    C．D．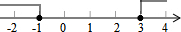

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

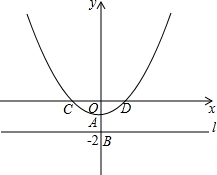    7．如图，在平面直角坐标系xOy中，直线l⊥y轴于点B（0，-2），A为OB的中点，以A为顶点的抛物线y=ax2+c与x轴交于C、D两点，且CD=4，点P为抛物线上的一个动点，以P为圆心，PO为半径画圆．
    （1）求抛物线的解析式；
    （2）若⊙P与y轴的另一交点为E，且OE=2，求点P的坐标；
    （3）判断直线l与⊙P的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

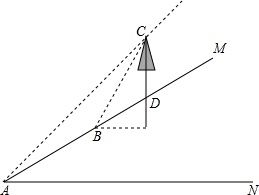    17．张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据：$\sqrt{3}$≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，在?ABCD中，O是对角线AC，BD的交点，下列结论错误的是（　　）
    A．AB∥CDB．AB=CDC．AC=BDD．OA=OC

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．设y=ax，若代数式（x+y）（x-2y）+3y（x+y）化简的结果为x2，请你求出满足条件的a值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小的长度为图形G1、G2的“密距”；当线段PQ的长度最大值时，我们称这个最大的长度为图形G1、G2的“疏距”．
    请你在学习、理解上述定义的基础上，解决下面的问题；
    在平面直角坐标系xOy中，点A的坐标为（-3，4），点B的坐标为（3，4），矩形ABCD的对称中心为点O．
    （1）线段AD和BC的“密距”是6，“疏距”是10；
    （2）设直线y=$\frac{3}{4}$x+b（b＞0）与x轴、y轴分别交于点E、F，若线段EF与矩形ABCD的“密距”是1，求它们的“疏距”；
    （3）平面直角坐标系xOy中有一个四边形KLMN，将矩形ABCD绕点O旋转一周，在旋转过程中，它与四边形KLMN的“疏距”的最大值为7，
    ①旋转过程中，它与四边形KLMN的“密距”的取值范围是1≤密距≤3；
    ②求四边形KLMN的面积的最大值．

    查看答案和解析>>

    同步练习册答案