
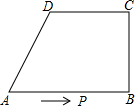
 在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=DC=3,P为梯形ABCD边上的一个动点,它从点A出发,以每秒1个单位的速度沿A→B→C→D运动.若设点P运动的时间为x秒,△APC的面积为S.则当x等于多少时,△APC的面积S=4.5?(如答案有多样,可根据需要,自行画图,并解答.)
在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=DC=3,P为梯形ABCD边上的一个动点,它从点A出发,以每秒1个单位的速度沿A→B→C→D运动.若设点P运动的时间为x秒,△APC的面积为S.则当x等于多少时,△APC的面积S=4.5?(如答案有多样,可根据需要,自行画图,并解答.) 分析 需要分类讨论:当点P在AB边上,点P在BC边上,点P在CD边上,根据三角形的面积公式求解可得.
解答 解: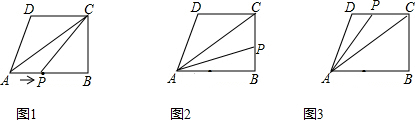
①如图1,当点P在AB边上时,S△APC=$\frac{1}{2}$AP•BC=$\frac{1}{2}$•x×3=4.5,
解得x=3,即当x=3时,△APC的面积S=4.5;
②如图2,当点P在BC边上时,S△APC=$\frac{1}{2}$PC•AB=$\frac{1}{2}$•(7-x)×4=4.5,
解得x=$\frac{19}{4}$,即当x=$\frac{19}{4}$时,△APC的面积S=4.5;
③如图,当点P在CD边上时,S△APC=$\frac{1}{2}$PC•BC=$\frac{1}{2}$•(x-7)×3=4.5,
解得x=10,即当x=10时,△APC的面积S=4.5;
综上所述,当x的值为3,$\frac{19}{4}$,10时,△APC的面积S=4.5.
点评 本题考查了动点函数图象.对于动点问题,需要分类讨论,以防漏解或错解.


科目:初中数学 来源: 题型:选择题
| A. | 45° | B. | 55° | C. | 45°或55° | D. | 55°或65° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 444>355>533 | B. | 533>444>355 | C. | 355>444>533 | D. | 355>533>444 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | mx+nx+k=(m+n)x+k | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)-3x | D. | (a+b)(a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{5x+3y=50+2}\\{11x+5y=90×0.9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+3y=50+2}\\{11x+5y=90÷0.9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+3y=50-2}\\{11x+5y=90×0.9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x+3y=50-2}\\{11x+5y=90÷0.9}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com