
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуP(2ЃЌ-2)дкЖўДЮКЏЪ§y=x2+mx+n(mЃО0)ЕФЭМЯѓЩЯЃЎ
(1)Шєm-n=3ЃЌЧѓmЁЂnЕФжЕЃЎ
(2)ШєИУЖўДЮКЏЪ§ЕФЭМЯѓгыyжсНЛгкЕуAЃЌЦфЖдГЦжсгыxжсНЛгкЕуBЃЌдђOA=OBГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ
(3)ШєИУЖўДЮКЏЪ§ЭМЯѓЯђзѓЦНвЦkИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ4mИіЕЅЮЛЃЌЫљЕУКЏЪ§ЭМЯѓШдОЙ§ЕуPЃЌЕБkЁн-2ЪБЃЌЧѓЫљЕУКЏЪ§ЭМЯѓЕФЖЅЕузнзјБъЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП(1)m=-1ЃЌn=-4ЃЛ(2)ВЛГЩСЂЃЛ(3)2ЃМ-![]() (m+4)2+2ЃМ1.
(m+4)2+2ЃМ1.
ЁОНтЮіЁП
(1)АбЕуP(2ЃЌ-2)ДњШыy=x2+mx+nЃЌЕУ2m+n=-6ЃЌНсКЯm-n=3МДПЩЧѓНтЃЛ
(2)гЩOA=OBЃЌЕУm=ЁР2nЃЌНсКЯ(1)жа2m+n=-6ЃЌЧѓНтm ЕФжЕЃЛ
(3)ЦНвЦКѓЕФКЏЪ§НтЮіЪНЮЊy=(x+k)2+m(x+k)-2m-2ЃЌP(2ЃЌ-2)дкЭМЯѓЩЯЃЌЕУЕНk(k+4+2m)=0Зжk=0КЭkЁй0ЬжТлЕУЕН0ЃМmЃМ-2ЃЌКЏЪ§ЖЅЕузнзјБъЮЊ![]() (m+4)2+2ЃЌНсКЯmЕФШЁжЕЗЖЮЇШЗЖЈзнзјБъШЁжЕЗЖЮЇЃЛ
(m+4)2+2ЃЌНсКЯmЕФШЁжЕЗЖЮЇШЗЖЈзнзјБъШЁжЕЗЖЮЇЃЛ
НтЃК(1)АбЕуP(2ЃЌ-2)ДњШыy=x2+mx+nЕУЃЌ
-2=4+2m+nЃЌ2m+n=-6
ЕБm-n=3ЪБЃЌНтЕУЃКm=-1ЃЌn=-4ЃЛ
(2)Сюx=0ЃЌдђy=nЃЌЁрA(0ЃЌn)ЃЌЁрOA=ЁРnЃЌ
КЏЪ§ЕФЖдГЦжсЮЊx=-![]() mЃЌOB=
mЃЌOB=![]() ЃЌ
ЃЌ
OA=OBЃЌдђЃКm=ЁР2nЃЌ
Ёп2m+n=-6ЃЌ
ЁрЕБm=2nЪБЃЌm=-![]() (ЩсШЅ)ЃЛ
(ЩсШЅ)ЃЛ
ЕБm=-2nЪБЃЌm=-4(ЩсШЅ)
ЙЪВЛГЩСЂЃЛ
(3)ЦНвЦКѓЕФКЏЪ§НтЮіЪНЮЊy=(x+k)2+m(x+k)+n+4
=(x+k)2+m(x+k)-6-2m+4
=(x+k)2+m(x+k)-2m-2ЃЌ
ЁпP(2ЃЌ-2)дкЭМЯѓЩЯЃЌ
Ёрk(k+4+2m)=0
ЕБk=0ЪБЃЌm=-2(ЩсШЅ)ЃЛ
ЕБkЁй0ЪБЃЌk=-4-2mЃЌ
ЁпkЁн-2ЃЌ
ЁрmЃМ-2ЃЌ
Ёр0ЃМmЃМ-2ЃЌ
ЁпКЏЪ§ЖЅЕузнзјБъЮЊ![]() =-
=-![]() (m+4)2+2ЃЌ
(m+4)2+2ЃЌ
Ёр-2ЃМ-![]() (m+4)2+2ЃМ1.
(m+4)2+2ЃМ1.


 Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
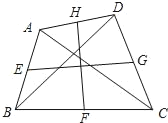
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌACЃНBDЃН8ЃЌEЁЂFЁЂGЁЂHЗжБ№ЪЧБпABЁЂBCЁЂCDЁЂDAЕФжаЕуЃЌдђEG2+FH2ЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊЕу
жаЃЌвбжЊЕу![]() ЃЈ2ЃЌ2ЃЉЃЌ
ЃЈ2ЃЌ2ЃЉЃЌ![]() ЃЈЃ1ЃЌ2ЃЉЃЌКЏЪ§
ЃЈЃ1ЃЌ2ЃЉЃЌКЏЪ§![]() .
.
ЃЈ1ЃЉЕБКЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕВЂЛГіжБЯп
ЕФжЕВЂЛГіжБЯп![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() СНЕужаЧЁгавЛИіЕуЕФзјБъЃЈ
СНЕужаЧЁгавЛИіЕуЕФзјБъЃЈ![]() ЃЌ
ЃЌ![]() ЃЉТњзуВЛЕШЪНзщ
ЃЉТњзуВЛЕШЪНзщ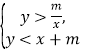 ЃЈ
ЃЈ![]() ЃО0ЃЉЃЌЧѓ
ЃО0ЃЉЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
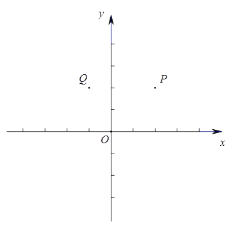
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЬЖгГаНгСЫ60ЭђЦНЗНУзЕФТЬЛЏЙЄГЬ,гЩгкЧщПігаБф,ЁЁЩшдМЦЛЎУПЬьТЬЛЏЕФУцЛ§ЮЊ![]() ЭђЦНЗНУз,СаЗНГЬЮЊ
ЭђЦНЗНУз,СаЗНГЬЮЊ![]() ,ИљОнЗНГЬПЩжЊЪЁТдЕФВПЗжЪЧЃЈ ЃЉ
,ИљОнЗНГЬПЩжЊЪЁТдЕФВПЗжЪЧЃЈ ЃЉ
A. ЪЕМЪЙЄзїЪБУПЬьЕФЙЄзїаЇТЪБШдМЦЛЎЬсИпСЫ![]() НсЙћЬсЧА30ЬьЭъГЩСЫетвЛШЮЮё
НсЙћЬсЧА30ЬьЭъГЩСЫетвЛШЮЮё
B. ЪЕМЪЙЄзїЪБУПЬьЕФЙЄзїаЇТЪБШдМЦЛЎЬсИпСЫ![]() ЃЌНсЙћбгЮѓ30ЬьЭъГЩСЫетвЛШЮЮё
ЃЌНсЙћбгЮѓ30ЬьЭъГЩСЫетвЛШЮЮё
C. ЪЕМЪЙЄзїЪБУПЬьЕФЙЄзїаЇТЪБШдМЦЛЎНЕЕЭСЫ![]() ЃЌНсЙћбгЮѓ30ЬьЭъГЩСЫетвЛШЮЮё
ЃЌНсЙћбгЮѓ30ЬьЭъГЩСЫетвЛШЮЮё
D. ЪЕМЪЙЄзїЪБУПЬьЕФЙЄзїаЇТЪБШдМЦЛЎНЕЕЭСЫ![]() ЃЌНсЙћЬсЧА30ЬьЭъГЩСЫетвЛШЮЮё
ЃЌНсЙћЬсЧА30ЬьЭъГЩСЫетвЛШЮЮё
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
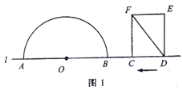
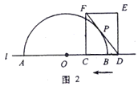
ЁОЬтФПЁПШчЭМ1,Еу![]() КЭОиаЮ
КЭОиаЮ![]() ЕФБп
ЕФБп![]() ЖМдкжБЯп
ЖМдкжБЯп![]() ЩЯ,вдЕу
ЩЯ,вдЕу![]() ЮЊдВаФ,вд24ЮЊАыОЖзїАыдВ,ЗжБ№НЛжБЯп
ЮЊдВаФ,вд24ЮЊАыОЖзїАыдВ,ЗжБ№НЛжБЯп![]() гк
гк![]() СНЕу.вбжЊ:
СНЕу.вбжЊ: ![]() ,
,![]() ,ОиаЮздгвЯђзѓдкжБЯп
,ОиаЮздгвЯђзѓдкжБЯп![]() ЩЯЦНвЦ,ЕБЕу
ЩЯЦНвЦ,ЕБЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЪБ,ОиаЮЭЃжЙдЫЖЏ.дкЦНвЦЙ§ГЬжа,ЩшОиаЮЖдНЧЯп
ЪБ,ОиаЮЭЃжЙдЫЖЏ.дкЦНвЦЙ§ГЬжа,ЩшОиаЮЖдНЧЯп![]() гыАыдВ
гыАыдВ![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() (Еу
(Еу![]() ЮЊАыдВЩЯдЖРыЕу
ЮЊАыдВЩЯдЖРыЕу![]() ЕФНЛЕу).
ЕФНЛЕу).
ЃЈ1ЃЉШчЭМ2ЃЌШє![]() гыАыдВ
гыАыдВ![]() ЯрЧаЃЌЧѓ
ЯрЧаЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
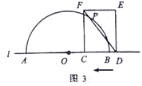
ЃЈ2ЃЉШчЭМ3ЃЌЕБ![]() гыАыдВ
гыАыдВ![]() гаСНИіНЛЕуЪБЃЌЧѓЯпЖЮ
гаСНИіНЛЕуЪБЃЌЧѓЯпЖЮ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШєЯпЖЮ![]() ЕФГЄЮЊ20ЃЌжБНгаДГіДЫЪБ
ЕФГЄЮЊ20ЃЌжБНгаДГіДЫЪБ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЃЈ1ЃЉе§ЗНаЮABCDМАЕШбќRtЁїAEFгаЙЋЙВЖЅЕуA,ЁЯEAFЃН90Ёу, СЌНгBEЁЂDF.НЋRtЁїAEFШЦЕуAа§зЊ,дка§зЊЙ§ГЬжаЃЌBEЁЂDFОпгадѕбљЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПНсКЯЭМ(1)ИјгшжЄУїЃЛ
(2)НЋЃЈ1ЃЉжаЕФе§ЗНаЮABCDБфЮЊОиаЮABCDЃЌЕШбќRtЁїAEFБфЮЊRtЁїAEFЃЌЧвADЃНkAB,AFЃНkAE,ЦфЫћЬѕМўВЛБф.(1)жаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПНсКЯЭМ(2)ЫЕУїРэгЩЃЛ
(3)НЋЃЈ2ЃЉжаЕФОиаЮABCDБфЮЊЦНааЫФБпаЮABCDЃЌНЋRtЁїAEFБфЮЊЁїAEFЃЌЧвЁЯBADЃНЁЯEAFЃН![]() ЃЌЦфЫћЬѕМўВЛБф.(2)жаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПНсКЯЭМ(3)ЃЌШчЙћВЛБфЃЌжБНгаДГіНсТлЃЛШчЙћБфЛЏЃЌжБНггУkБэЪОГіЯпЖЮBEЁЂDFЕФЪ§СПЙиЯЕЃЌгУ
ЃЌЦфЫћЬѕМўВЛБф.(2)жаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПНсКЯЭМ(3)ЃЌШчЙћВЛБфЃЌжБНгаДГіНсТлЃЛШчЙћБфЛЏЃЌжБНггУkБэЪОГіЯпЖЮBEЁЂDFЕФЪ§СПЙиЯЕЃЌгУ![]() БэЪОГіжБЯпBEЁЂDFаЮГЩЕФШёНЧ
БэЪОГіжБЯпBEЁЂDFаЮГЩЕФШёНЧ![]() .
.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжабЇЩњЩЯЭјЯжЯѓдНРДдНЪмЕНЩчЛсЕФЙизЂЃЌаЁМЧепаЁЛлЫцЛњЕїВщСЫФГаЃШєИЩбЇЩњКЭМвГЄЖдЩЯЭјЯжЯѓЕФПДЗЈжЦзїСЫШчЯТЕФЭГМЦЭМ1КЭ2ЃЎЧыИљОнЯрЙиаХЯЂЃЌНтД№ЛђВЙШЋЯТСаЮЪЬтЃЎ

ЃЈ1ЃЉВЙШЋЭМ1ЃЛ
ЃЈ2ЃЉЧѓЭМ2жаБэЪОМвГЄЁАдоГЩЁБЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИУаЃЙВга1600УћбЇЩњЃЌЧыФуЙРМЦетЫљжабЇЕФЫљгабЇЩњжаЃЌЖдЩЯЭјГжЁАЗДЖдЁБЬЌЖШЕФгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌгыyжсНЛгкЕуBЃЌгыХзЮяЯп
ЃЌгыyжсНЛгкЕуBЃЌгыХзЮяЯп![]() ЕФЖдГЦжсНЛгкЕу
ЕФЖдГЦжсНЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ3ЃЉ![]() ЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌЙ§ЕуNзїДЙжБгкyжсЕФжБЯпгыХзЮяЯпНЛгкЕу
ЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌЙ§ЕуNзїДЙжБгкyжсЕФжБЯпгыХзЮяЯпНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЈЕуPдкЕуQЕФзѓВрЃЉЃЎШє
ЃЈЕуPдкЕуQЕФзѓВрЃЉЃЎШє![]() КуГЩСЂЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
КуГЩСЂЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁгУ36000дЊЙКНјМзЁЂввСНжжЩЬЦЗЃЌЯњЪлЭъКѓЙВЛёРћ6000дЊЃЎЦфжаМзжжЩЬЦЗУПМўНјМл120дЊЃЌЪлМл138дЊЃЛввжжЩЬЦЗУПМўНјМл100дЊЃЌЪлМл120дЊЃЎ
ЃЈ1ЃЉИУЩЬГЁЙКНјМзЁЂввСНжжЩЬЦЗИїЖрЩйМўЃП
ЃЈ2ЃЉЩЬГЁЕкЖўДЮвддНјМлЙКНјМзЁЂввСНжжЩЬЦЗЃЌЙКНјввжжЩЬЦЗЕФМўЪ§ВЛБфЃЌЖјЙКНјМзжжЩЬЦЗЕФМўЪ§ЪЧЕквЛДЮЕФ2БЖЃЌМзжжЩЬЦЗАДдЪлМлГіЪлЃЌЖјввжжЩЬЦЗДђелЯњЪлЃЎШєСНжжЩЬЦЗЯњЪлЭъБЯЃЌвЊЪЙЕкЖўДЮОгЊЛюЖЏЛёРћВЛЩйгк8160дЊЃЌввжжЩЬЦЗзюЕЭЪлМлЮЊУПМўЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com