
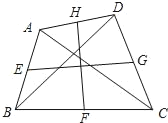
【题目】如图,在四边形ABCD中,AC=BD=8,E、F、G、H分别是边AB、BC、CD、DA的中点,则EG2+FH2的值为_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
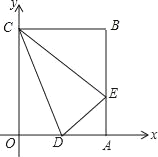
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点M为二次函数y=﹣x2+2bx+1+4b﹣b2图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否恒在某条直线上?若是,求出该直线解析式;若不是,说明理由.
(2)若二次函数图象也经过点A,B,且mx+5>﹣x2+2bx+2+4b﹣b2,借助图象,求出x的取值范围.
(3)点A坐标为(5,0),点M在△AOB内时,若点C(![]() ,y1),D(
,y1),D(![]() ,y2)都在二次函数图象上,试比较y1与y2的大小.
,y2)都在二次函数图象上,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
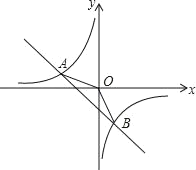
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=![]() (m为常数,且m≠0)的图象交于点A(﹣4,2),B(2,n).
(m为常数,且m≠0)的图象交于点A(﹣4,2),B(2,n).
(1)求反比例函数和一次函数的解析式.
(2)连接OA,OB,求△AOB的面积.
(3)直接写出当0<y1<y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
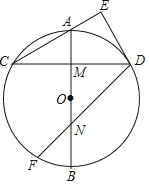
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在![]() 上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
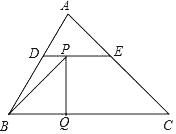
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE=![]() ,BC=
,BC=![]() .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
.动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )
A. 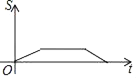 B.
B. 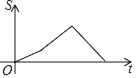
C. 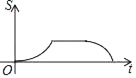 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
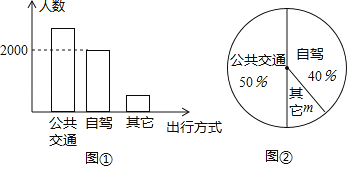
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(2,-2)在二次函数y=x2+mx+n(m>0)的图象上.
(1)若m-n=3,求m、n的值.
(2)若该二次函数的图象与y轴交于点A,其对称轴与x轴交于点B,则OA=OB成立吗?请说明理由.
(3)若该二次函数图象向左平移k个单位,再向上平移4m个单位,所得函数图象仍经过点P,当k≥-2时,求所得函数图象的顶点纵坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com