
【题目】某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.
根据所给信息,解答以下问题:
(1)在这次调查中一共抽取了 名学生;
(2)在扇形统计图中,C对应的扇形的圆心角是 度;
(3)补全条形统计图;
(4)所抽取学生的足球运球测试成绩的中位数落在 等级;
(5)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

【答案】(1)40;(2)117;(3)补全的条形统计图如图所示;见解析;(4)B;(5)足球运球测试成绩达到A级的学生有30人.
【解析】
(1)根据B等级的学生数和所占的百分比可以求得本次调查的学生数;
(2)根据(1)中的结果可以求得在扇形统计图中,C对应的扇形的圆心角的度数;
(3)根据(1)中的结果可以求得C等级的人数,从而可以将条形统计图补充完整;
(4)根据统计图中的数据可以得到所抽取学生的足球运球测试成绩的中位数落在哪个等级;
(5)根据统计图中的数据可以求得足球运球测试成绩达到A级的学生有多少人.
(1)18÷45%=40,
即在这次调查中一共抽取了40名学生,
故答案为:40;
(2)在扇形统计图中,C对应的扇形的圆心角是:360°×![]() =117°,
=117°,
故答案为:117;
(3)C等级的人数为:40﹣4﹣18﹣5=13,
补全的条形统计图如图所示;

(4)由统计图可知,
所抽取学生的足球运球测试成绩的中位数落在B等级,
故答案为:B;
(5)300×![]() =30(人),
=30(人),
答:足球运球测试成绩达到A级的学生有30人.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】(1)方法形成
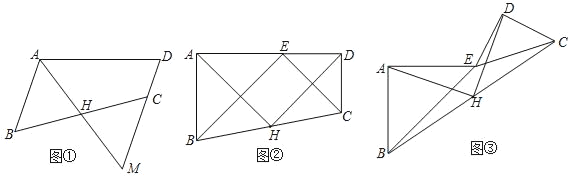
如图①,在四边形ABCD中,AB∥DC,点H是BC的中点,连结AH并延长交DC的延长线于M,则有CM=AB.请说明理由;
(2)方法迁移
如图②,在四边形ABCD中,点H是BC的中点,E是AD上的点,且△ABE和△DEC都是等腰直角三角形,∠BAE=∠EDC=90°.请探究AH与DH之间的关系,并说明理由.
(3)拓展延伸
在(2)的条件下,将Rt△DEC绕点E旋转到图③的位置,请判断(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD·AB;
(3)若⊙O的半径为2,∠ACD=300,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
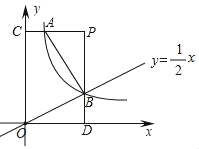
【题目】如图,双曲线y=![]() (x>0)的图象经过点A(
(x>0)的图象经过点A(![]() ,4),直线y=
,4),直线y=![]() x与双曲线交于B点,过A,B分别作y轴、x轴的垂线,两线交于P点,垂足分别为C,D.
x与双曲线交于B点,过A,B分别作y轴、x轴的垂线,两线交于P点,垂足分别为C,D.
(1)求双曲线的解析式;
(2)求证:△ABP∽△BOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B. 假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C. 如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D. 转动转盘20次,一定有6次获得“文具盒”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且∠DAE=![]() α.
α.
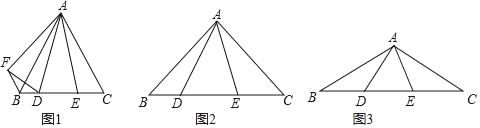
(1)如图1,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF,
①求∠DAF的度数;
②求证:△ADE≌△ADF;
(2)如图2,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由;
(3)如图3,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com