
【题目】“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B. 假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C. 如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D. 转动转盘20次,一定有6次获得“文具盒”
科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2交x轴负半轴于点A(﹣1,0),与y轴交于B点.过B点的直线l交抛物线于点C(3,﹣1).过点C作CD⊥x轴,垂足为D.点P为x轴正半轴上的动点,过P点作x轴的垂线,交直线l于点E,交抛物线于点F.设P点的横坐标为t.
(1)求抛物线的解析式;
(2)连接OE,求△POE面积的最大值;
(3)连接DE,CF,是否存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.
根据所给信息,解答以下问题:
(1)在这次调查中一共抽取了 名学生;
(2)在扇形统计图中,C对应的扇形的圆心角是 度;
(3)补全条形统计图;
(4)所抽取学生的足球运球测试成绩的中位数落在 等级;
(5)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
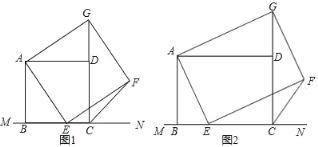
【题目】如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)
(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某学校为构建书香校园,拟购进甲、乙两种规格的书柜放置新购置的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用3600元购进的甲种书柜的数量比用4200元购进的乙种书柜的数量少4台.
(1)求甲、乙两种书柜的进价;
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.请您帮该校设计一种购买方案,使得花费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为( )
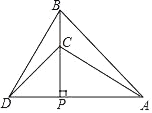
A. 5B. 10C. l5D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com