
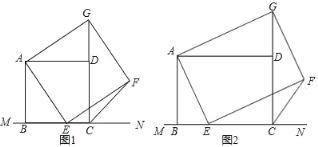
【题目】如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)
(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.
【答案】(1)见解析;(2)∠FCN=45°,理由见解析;(3)当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=![]() .理由见解析.
.理由见解析.
【解析】
(1)根据三角形判定方法进行证明即可.
(2)作FH⊥MN于H.先证△ABE≌△EHF,得到对应边相等,从而推出△CHF是等腰直角三角形,∠FCH的度数就可以求得了.
(3)解法同(2),结合(1)(2)得:△EFH≌△GAD,△EFH∽△ABE,得出EH=AD=BC=8,由三角函数定义即可得出结论.
(1)证明:∵四边形ABCD和四边形AEFG是正方形,
∴AB=AD,AE=AG=EF,∠BAD=∠EAG=∠ADC=90°,
∴∠BAE+∠EAD=∠DAG+∠EAD,∠ADG=90°=∠ABE,
∴∠BAE=∠DAG,
在△ADG和△ABE中,
 ,
,
∴△ADG≌△ABE(AAS).
(2)解:∠FCN=45°,理由如下:
作FH⊥MN于H,如图1所示:
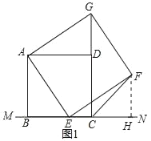
则∠EHF=90°=∠ABE,
∵∠AEF=∠ABE=90°,
∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠FEH=∠BAE,在△EFH和△ABE中,
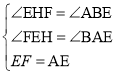 ,
,
∴△EFH≌△ABE(AAS),
∴FH=BE,EH=AB=BC,
∴CH=BE=FH,
∵∠FHC=90°,
∴∠FCN=45°.
(3)当点E由B向C运动时,∠FCN的大小总保持不变,理由如下:
作FH⊥MN于H,如图2所示:
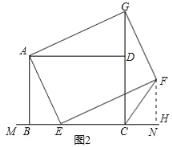
由已知可得∠EAG=∠BAD=∠AEF=90°,
结合(1)(2)得:△EFH≌△GAD,△EFH∽△ABE,
∴EH=AD=BC=8,
∴CH=BE,
∴![]() ;
;
在Rt△FEH中,tan∠FCN=![]() ,
,
∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=![]() .
.


科目:初中数学 来源: 题型:
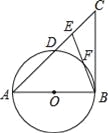
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
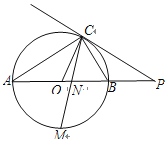
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒中装有编号为1,2,3三个球,乙盒中装有编号为4,5,6三个球,每个盒子中的球除编号外其它完全相同,将盒子中的球摇均后,从每个盒子中随机各取一个球.
(1)从甲盒中取出的球号数是3的概率是 ;
(2)请用列表法或画树状图法,求从两个盒子中取出的球号数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
下列说法不正确的是( )

A. 当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B. 假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C. 如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D. 转动转盘20次,一定有6次获得“文具盒”
查看答案和解析>>
科目:初中数学 来源: 题型:
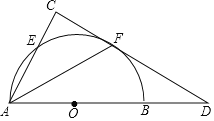
【题目】如图,已知AB是⊙O的直径,⊙O与Rt△ACD的两直角边分别交于点E、F,点F是弧BE的中点,∠C=90°,连接AF.
(1)求证:直线DF是⊙O的切线.
(2)若BD=1,OB=2,求tan∠AFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
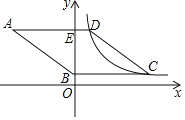
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
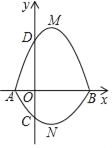
【题目】如图,抛物线C1:y=mx2﹣2mx﹣3m(m<0)与x轴交于A、B两点,与y轴交于点D,顶点为M,另一条抛物线C2与x轴也交于A、B两点,且与y轴的交点是C(0,![]() ),顶点是N.
),顶点是N.
(1)求A,B两点的坐标.
(2)求抛物线C2的函数表达式.
(3)是否存在m,使得△OBD与△OBC相似?若存在,请求出m的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com