
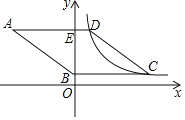
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
科目:初中数学 来源: 题型:
【题目】某校为了了解学生“最喜爱的运动项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
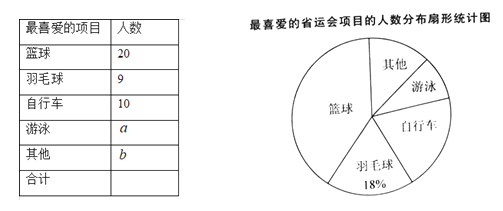
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,a+b= .
(2)扇形统计图中“自行车”对应的扇形的圆心角为 .
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2交x轴负半轴于点A(﹣1,0),与y轴交于B点.过B点的直线l交抛物线于点C(3,﹣1).过点C作CD⊥x轴,垂足为D.点P为x轴正半轴上的动点,过P点作x轴的垂线,交直线l于点E,交抛物线于点F.设P点的横坐标为t.
(1)求抛物线的解析式;
(2)连接OE,求△POE面积的最大值;
(3)连接DE,CF,是否存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)
(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.
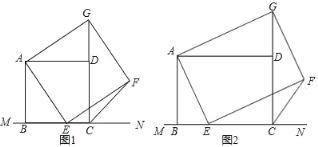
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某学校为构建书香校园,拟购进甲、乙两种规格的书柜放置新购置的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用3600元购进的甲种书柜的数量比用4200元购进的乙种书柜的数量少4台.
(1)求甲、乙两种书柜的进价;
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.请您帮该校设计一种购买方案,使得花费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
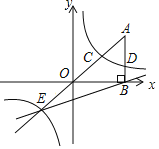
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com