

���� ��1����ͼ1�У���A��AG��BC��G��ֻҪ֤����DAC=2��ADE����BAD=2��ADF���ɽ�����⣮
��2�����ۣ�CM=2PQ������֤���ı���AMNQ����һ���ڽ�Ϊ60������Σ���MN��AC��QN��AB���Ƴ�$\frac{PN}{NC}$=$\frac{AQ}{QC}$=$\frac{PM}{AM}$����$\frac{MQ}{CM}$=$\frac{PM}{MQ}$����Ϊ��PMQ=��MQC�����ԡ�PMQ�ס�MQC�����ԡ�MQP=��MCQ��$\frac{PQ}{CM}$=$\frac{MQ}{CQ}$����Ϊ��QMO=��CMQ�����ԡ�MOQ�ס�MQC������$\frac{OM}{MQ}$=$\frac{OQ}{CQ}$������$\frac{MQ}{CQ}$=$\frac{OM}{OQ}$=$\frac{1}{2}$���ɴ˽�����⣮
��� ��1��֤������ͼ1�У���A��AG��BC��G��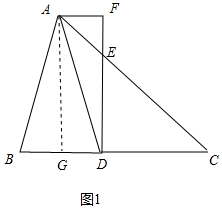
��AF��BC��DF��BC��
��DF��AF��
���ı���AGDF�Ǿ��Σ�
��AF=DG��
��BD=2AF��
��BG=DG��
��AB=AD��
���BAG=��DAG��
�ߡ�DEC=3��ADE=��ADE+��DAE��
���DAE=2��ADE��
��AG��DF��
���GAD=��ADE��
���DAE=2��DAG��
�ߡ�BAD=2��DAG��
���BAD=��DAE��
��ADƽ�֡�BAC��
��2���⣺���ۣ�CM=2PQ��
���ɣ�����MN��QN��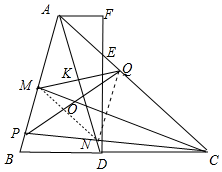
��ADƽ�֡�BAC��
���KAM=��KAQ����AKM=��AKQ=90�㣬AK=AK��
���AKM�ա�AKQ��
��AM=AQ���ߡ�MAQ=60�㣬
���AMQ�ǵȱ������Σ�
��AM=MQ=AQ��MK=KQ����AMQ=��AQM=60�㣬
���PMQ=��MQC=120�㣬
��AN��MQ���ഹֱƽ�֣�
���ı���AMNQ�����Σ�
��MN��AC��QN��AB��
��$\frac{PN}{NC}$=$\frac{AQ}{QC}$=$\frac{PM}{AM}$����$\frac{MQ}{CM}$=$\frac{PM}{MQ}$���ߡ�PMQ=��MQC��
���PMQ�ס�MQC��
���MQP=��MCQ��$\frac{PQ}{CM}$=$\frac{MQ}{CQ}$��
�ߡ�QMO=��CMQ��
���MOQ�ס�MQC��
��$\frac{OM}{MQ}$=$\frac{OQ}{CQ}$��
��$\frac{MQ}{CQ}$=$\frac{OM}{OQ}$=$\frac{1}{2}$��
��$\frac{PQ}{CM}$=$\frac{MQ}{CQ}$=$\frac{1}{2}$��
��CM=2PQ��
���� ���⿼�����������ε��ж������ʡ��ȱ������ε��ж������ʡ����ε��ж������ʣ�ƽ���߷��߶γɱ���������֪ʶ������Ĺؼ������Ӧ�����������ε��ж���Ѱ�������������DZ�����ѵ㣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼA��B��C��D�ڡ�O�ϣ���֪AB=10��CD=6����A+��C=90�㣬���O�İ뾶=$\sqrt{34}$��
��ͼA��B��C��D�ڡ�O�ϣ���֪AB=10��CD=6����A+��C=90�㣬���O�İ뾶=$\sqrt{34}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{3}$��-$\sqrt{3}$ | C�� | $\sqrt{3}$��5 | D�� | -$\sqrt{3}$��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com