
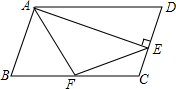
 已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )
已知?ABCD中,AD=2AB,F是BC的中点,作AE⊥CD,垂足E在线段CD上,连结EF、AF,下列结论:①2∠BAF=∠BAD;②EF=AF;③S△ABF≤S△AEF;④∠BFE=3∠CEF.中一定成立的是( )| A. | ①②④ | B. | ①③ | C. | ②③④ | D. | ①②③④ |
分析 利用平行四边形的性质:平行四边形的对边相等且平行,再由全等三角形的判定得出△MBF≌△ECF,利用全等三角形的性质得出对应线段之间关系进而得出答案.
解答 解:①∵F是BC的中点,
∴BF=FC,
∵在?ABCD中,AD=2AB,
∴BC=2AB=2CD,∴BF=FC=AB,
∴∠AFB=∠BAF,
∵AD∥BC,
∴∠AFB=∠DAF,
∴∠BAF=∠FAB,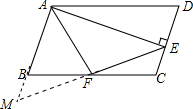
∴2∠BAF=∠BAD,故①正确;
②延长EF,交AB延长线于M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠MBF=∠C,
∵F为BC中点,
∴BF=CF,
在△MBF和△ECF中,
$\left\{\begin{array}{l}{∠MBF=∠C}\\{BF=CF}\\{∠BFM=∠CFE}\end{array}\right.$,
∴△MBF≌△ECF(ASA),
∴FE=MF,∠CEF=∠M,
∵CE⊥AE,
∴∠AEC=90°,
∴∠AEC=∠BAE=90°,
∵FM=EF,
∴EF=AF,故②正确;
③∵EF=FM,
∴S△EFC=S△AFM,
∴S△ABF≤S△AEF,故③正确;
④设∠FEA=x,则∠FAE=x,
∴∠BAF=∠AFB=90°-x,
∴∠EFA=180°-2x,
∴∠EFB=90°-x+180°-2x=270°-3x,
∵∠CEF=90°-x,
∴∠BFE=3∠CEF,故④正确,
故选:D.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,解决本题的关键是得出△AEF≌△DME.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 画出函数y=x-3的图象,并根据图象指出:
画出函数y=x-3的图象,并根据图象指出:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
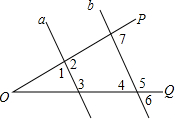 如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )
如图,已知直线a∥b,同时与∠POQ的两边相交,则下列结论中错误的是( )| A. | ∠3+∠4=180° | B. | ∠2+∠5>180° | C. | ∠1+∠6<180° | D. | ∠2+∠7=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
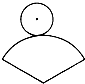 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )| A. | 2$\sqrt{2}$r | B. | r | C. | $\sqrt{10}$r | D. | 3r |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
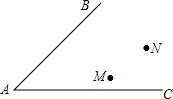 如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使PM=PN.有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个茶水供应点的位置就确定了”,你认为这位同学说得对吗?请说明理由,并通过作图找出这一点,不写作法,保留作图痕迹.
如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个饮水供应点P,使P到两条道路的距离相等,且使PM=PN.有一同学说:“只要作一个角平分线、一条线段的垂直平分线,这个茶水供应点的位置就确定了”,你认为这位同学说得对吗?请说明理由,并通过作图找出这一点,不写作法,保留作图痕迹.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com