
【题目】已知a,b,c为有理数,且它们在数轴上的位置如图所示.
![]()
(1)试判断a,b,c的正负性;
(2)根据数轴化简:
①|a|=_____; ②|b|=_____:
③|c|=_____; ④|-a|=_____;
⑤|-b|=_____; ⑥|-c|=_____.
(3)若|a|=5.5,|b|=2.5,|c|=5,求a,b,c的值.
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. 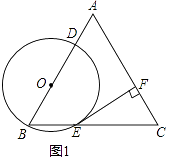
(1)求证:直线EF是⊙O的切线;
(2)如图2,当直线AC与⊙O相切时,求⊙O的半径. 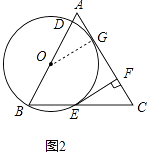
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,在△ABC的外部作∠ACM,使得∠ACM=![]() ∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D是直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
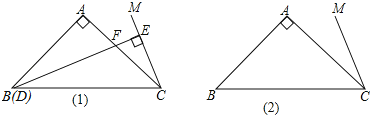
(1)如图1所示,当点D与点B重合时,延长BA,CM交点N,证明:DF=2EC;
(2)当点D在直线BC上运动时,DF和EC是否始终保持上述数量关系呢?请你在图2中画出点D运动到CB延长线上某一点时的图形,并证明此时DF与EC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB=2 ![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚同学动手剪了如图①所示的正方形与长方形纸片若干张.

(1)他用1张1号、1张2号和2张3号卡片拼出一个新的图形(如图②).根据这个图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是 ;
(2)如果要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要2号卡片 张,3号卡片 张;
(3)当他拼成如图③所示的长方形,根据6张小纸片的面积和等于打纸片(长方形)的面积可以把多项式a2+3ab+2b2分解因式,其结果是 ;
(4)动手操作,请你依照小刚的方法,利用拼图分解因式a2+5ab+6b2= 画出拼图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com