
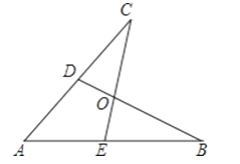
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中, 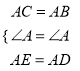 ,
,
∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中, 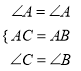 ,
,
∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中, 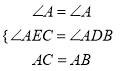 ,
,
∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点睛:本题考查了全等三角形的判定方法,是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.
【题型】填空题
【结束】
17
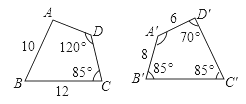
【题目】如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________,∠A=________,B′C′=________,AD=________.
科目:初中数学 来源: 题型:
【题目】一块长105m、宽60m的长方形土地如下图所示.
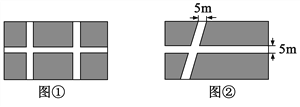
(1)上面修了两条平行且与第三条垂直的小路,宽都是5m,如图①,将阴影部分种上草坪,则草坪的面积是多少?
(2)小明在解决问题后发现:把小路改为如图②所示的平行四边形的形状,草坪的面积不变,你同意他的观点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
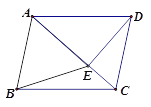
【题目】如图,在四边形ABCD中,AB//CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE .
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长 .
,求对角线AC的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是( ).
A. 当m=0时,x1=2,x2=3
B. m>﹣![]()
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
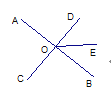
【题目】如图3,直线AB、CD相交于O,若∠AOD比∠AOC大40°,则∠BOD=___°;若∠AOD=2∠AOC,则∠BOC=___;若∠AOD=∠AOC,则∠BOD=___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com