【题目】如图，∠MON=30°，点A1 ， A2 ， A3 ， …在射线ON上，点B1 ， B2 ， B3 ， …在射线OM上，△A1B1A2 ， △A2B2A3 ， △A3B3A4…均为等边三角形．若OA1=1，则△AnBnAn+1的边长为 ． 
【答案】2n﹣1
【解析】解：∵△A1B1A2是等边三角形， ∴A1B1=A2B1 ， ∠3=∠4=∠12=60°，
∴∠2=120°，
∵∠MON=30°，
∴∠1=180°﹣120°﹣30°=30°，
又∵∠3=60°，
∴∠5=180°﹣60°﹣30°=90°，
∵∠MON=∠1=30°，
∴OA1=A1B1=1，
∴A2B1=1，
∵△A2B2A3、△A3B3A4是等边三角形，
∴∠11=∠10=60°，∠13=60°，
∵∠4=∠12=60°，
∴A1B1∥A2B2∥A3B3 ， B1A2∥B2A3 ，
∴∠1=∠6=∠7=30°，∠5=∠8=90°，
∴A2B2=2B1A2 ， B3A3=2B2A3 ，
∴A3B3=4B1A2=4，
A4B4=8B1A2=8，
A5B5=16B1A2=16，
以此类推：△AnBnAn+1的边长为 2n﹣1 ．
故答案是：2n﹣1 ．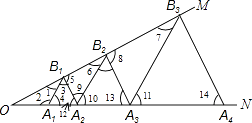 
【考点精析】通过灵活运用等边三角形的性质，掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题．
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案科目：初中数学 来源： 题型：
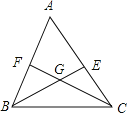
【题目】如图，已知△ABC的∠ABC和∠ACB的平分线BE，CF交于点G，若∠BGC=115°，则∠A= ．
【答案】50°
【解析】
试题分析：根据三角形内角和定理求出∠GBC+∠GCB，根据角平分线的定义求出∠ABC+∠ACB，根据三角形内角和定理计算即可．
解：∵∠BGC=115°，
∴∠GBC+∠GCB=180°﹣115°=65°，
∵BE，CF是△ABC的∠ABC和∠ACB的平分线，
∴∠GBC=
ABC，∠GCB=ACB，
∴∠ABC+∠ACB=130°，
∴∠A=180°﹣130°=50°，
故答案为：50°．
【题型】填空题
【结束】
14
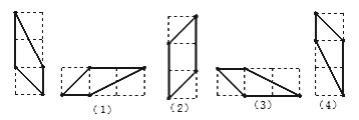
【题目】如图所示，有（1）～（4）4个条形方格图，图中由实线围成的图形与前图全等的有
________（只要填序号即可）．
查看答案和解析>>
科目：初中数学 来源： 题型：
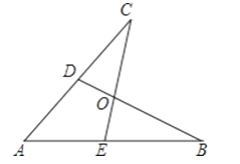
【题目】如图所示，E，D是AB，AC上的两点，BD，CE交于点O，且AB=AC，使△ACE≌△ABD，你补充的条件是________
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC；理由如下：
若AD=AE，
在△ACE和△ABD中，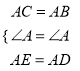 
，
∴△ACE≌△ABD（SAS）；
若CD=BE，
∵AB=AC，
∴AD=AE，
同理：△ACE≌△ABD（SAS）；
若∠B=∠C，
在△ACE和△ABD中，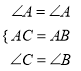 
，
∴△ACE≌△ABD（ASA）；
若∠ADB=∠AEC，
在△ACE和△ABD中，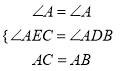 
，
∴△ACE≌△ABD（AAS）；
故答案为：AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC．
点睛：本题考查了全等三角形的判定方法，是开放型题目，存在四种情况，熟练掌握全等三角形的判定方法是解决问题的关键．
【题型】填空题
【结束】
17
【题目】如图，四边形ABCD与四边形A′B′C′D′全等，则∠A′=________，∠A=________，B′C′=________，AD=________．
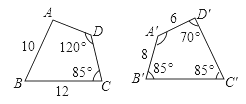
查看答案和解析>>
科目：初中数学 来源： 题型：
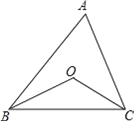
【题目】如图，已知点O是△ABC的两条角平分线的交点，
（1）若∠A=30°，则∠BOC的大小是 ；
（2）若∠A=60°，则∠BOC的大小是 ；
（3）若∠A=n°，则∠BOC的大小是多少？试用学过的知识说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车的速度为120千米/时，乙车的速度为80千米/时，t时后两车相距50千米，则t的值为____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下调查中，应采用全面调查的是（ ）
A.调查某批次汽车的抗撞击能力
B.了解全国中学生的视力和用眼卫生情况
C.了解某班学生的身高情况
D.调查某池塘中现有鱼的数量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
