
【题目】若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是( ).
A. 当m=0时,x1=2,x2=3
B. m>﹣![]()
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
【答案】C
【解析】试题分析:根据方程的解的定义可以判定A正确;根据二次函数的最值问题,且结合题意可以判定B正确;根据二次函数与x轴交点的有关性质可以判定C错误;根据二次函数的定义可以判定D正确.①∵m=0时,方程为(x﹣2)(x﹣3)=0,∴x1=2,x2=3,故A正确;②设y=(x﹣2)(x﹣3)=x2﹣5x+6=(x﹣![]() )2﹣
)2﹣![]() ,∴y的最小值为﹣
,∴y的最小值为﹣![]() ,∵一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1<x2,∴m>﹣
,∵一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1<x2,∴m>﹣![]() ,故B正确;③∵m>O时,y=(x﹣2)(x﹣3)>0,函数y′=(x﹣2)(x﹣3)﹣m与x轴交于(x1,0),(x2,0),∴x1<2<3<X2,故C错误;④∵y=(x﹣x1)(x﹣x2)+m=(x﹣2)(x﹣3)﹣m+m=(x﹣2)(x﹣3),∴函数与x轴交于点(2,0),(3,0).故D正确.故选C.
,故B正确;③∵m>O时,y=(x﹣2)(x﹣3)>0,函数y′=(x﹣2)(x﹣3)﹣m与x轴交于(x1,0),(x2,0),∴x1<2<3<X2,故C错误;④∵y=(x﹣x1)(x﹣x2)+m=(x﹣2)(x﹣3)﹣m+m=(x﹣2)(x﹣3),∴函数与x轴交于点(2,0),(3,0).故D正确.故选C.


科目:初中数学 来源: 题型:
【题目】(本题满分8分)我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
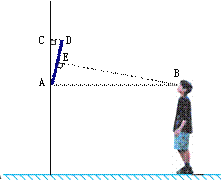
求:⑴ 装饰画与墙壁的夹角∠CAD的度数(精确到1°);
⑵ 装饰画顶部到墙壁的距离DC(精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
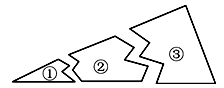
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析:根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形.
故选C.
考点:全等三角形的应用.
【题型】单选题
【结束】
12
【题目】如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为________m,依据是________
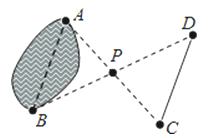
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
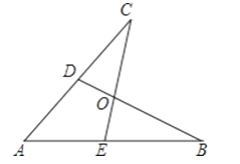
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中, 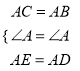 ,
,
∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中, 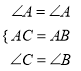 ,
,
∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中, 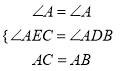 ,
,
∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点睛:本题考查了全等三角形的判定方法,是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.
【题型】填空题
【结束】
17
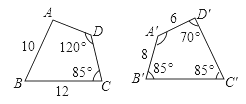
【题目】如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________,∠A=________,B′C′=________,AD=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
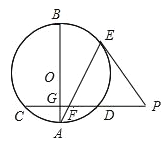
(1)求证:PE=PF
(2)已知AG=4,AF=5,EF=25,求圆O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com