
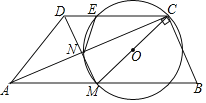
【题目】如图,在Rt△ABC中,M是斜边AB的中点,以CM为直径作圆O交AC于点N,延长MN至D,使ND=MN,连接AD、CD,CD交圆O于点E.
(1)判断四边形AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求BC的长.
【答案】(1)四边形AMCD是菱形,理由见解析;(2)证明见解析;(3)BC=2![]() .
.
【解析】
(1)证明四边形AMCD的对角线互相平分,且∠CNM=90°,可得四边形AMCD为菱形;
(2)可证得∠CMN=∠DEN,由CD=CM可证出∠CDM=∠CMN,则∠DEN=∠CDM,结论得证;
(3)证出△MDC∽△EDN,由比例线段可求出ND长,再求MN的长,则BC可求出.
(1)四边形AMCD是菱形,理由如下:
∵M是Rt△ABC中AB的中点,
∴CM=AM,
∵CM为⊙O的直径,
∴∠CNM=90°,
∴MD⊥AC,
∴AN=CN,
∵ND=MN,
∴四边形AMCD是菱形;
(2)∵四边形CENM为⊙O的内接四边形,
∴∠CEN+∠CMN=180°,
∵∠CEN+∠DEN=180°,
∴∠CMN=∠DEN,
∵四边形AMCD是菱形,
∴CD=CM,
∴∠CDM=∠CMN,
∴∠DEN=∠CDM,
∴ND=NE;
(3)∵∠CMN=∠DEN,∠MDC=∠EDN,
∴△MDC∽△EDN,
∴![]() ,
,
设DN=x,则MD=2x,由此得![]() ,
,
解得:x=![]() 或x=﹣
或x=﹣![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() ,
,
∵MN为△ABC的中位线,
∴BC=2MN,
∴BC=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资. 已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为120元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元)。(年获利=年销售额—生产成本—投资)
(万元)。(年获利=年销售额—生产成本—投资)
(1)试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请通过计算说明,到第一年年底,当![]() 取最大值时,销售单价
取最大值时,销售单价![]() 定为多少?此时公司是盈利了还是亏损了?
定为多少?此时公司是盈利了还是亏损了?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校七年级4个班共180人的体质健康情况,从各班分别抽取同样数量的男生和女生组成一个样本,如图是根据样本绘制的条形图和扇形图.
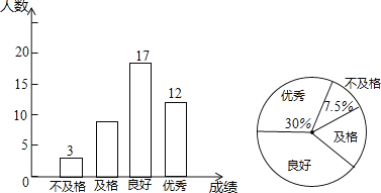
(1)本次抽查的样本容量是______.
(2)请补全条形图和扇形图中的百分数;
(3)请你估计全校七年级共有多少人优秀.
查看答案和解析>>
科目:初中数学 来源: 题型:
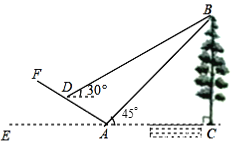
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
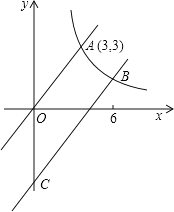
【题目】如图,直线OA与反比例函数的图象交于点A(3,3),向下平移直线OA,与反比例函数的图象交于点B(6,m)与y轴交于点C,
(1)求直线BC的解析式;
(2)求经过A、B、C三点的二次函数的解析式;
(3)设经过A、B、C三点的二次函数图象的顶点为D,对称轴与x轴的交点为E.
问:在二次函数的对称轴上是否存在一点P,使以O、E、P为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P1(﹣1,y1),P2(2,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
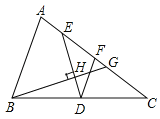
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com