

分析 (1)读图可知喜欢足球的有40人,占20%,求出总人数;
(2)根据总人数求出喜欢乒乓球的人数所占的百分比,得出喜欢排球的人数,再根据喜欢篮球的人数所占的百分比求出喜欢篮球的人数,从而补全统计图;
(3)用列表法求出总的事件所发生的数目,再根据概率公式即可求出刚好抽到一男一女的概率.
解答 解:(1)∵喜欢足球的有40人,占20%,
∴一共调查了:40÷20%=200(人),
故答案为:200;
(2)∵喜欢乒乓球人数为60人,
∴所占百分比为:$\frac{60}{200}$×100%=30%,
∴喜欢排球的人数所占的百分比是1-20%-30%-40%=10%
∴喜欢排球的人数为:200×10%=20(人),
∴喜欢篮球的人数为200×40%=80(人),
由以上信息补全条形统计图得: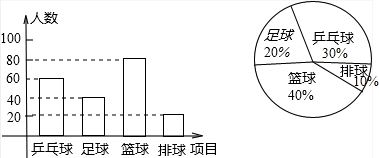
(3)列表或画树状图如下:
| 女1 | 女2 | 女3 | 男1 | 男2 | |
| 女1 | (女2,女1) | (女3,女1) | (男1,女1) | (男2,女1) | |
| 女2 | (女1,女2) | (女3,女2) | (男1,女2) | (男2,女2) | |
| 女3 | (女1,女3) | (女2,女3) | (男1,女3) | (男2,女3) | |
| 男1 | (女1,男1) | (女2,男1) | (女3,男1) | (男1,男1) | |
| 男2 | (女1,男2) | (女2,男2) | (女3,男2) | (男1,男2) |
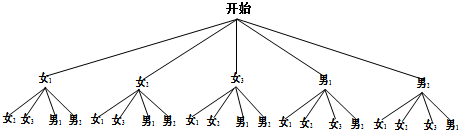
点评 本题考查学生的读图能力和求随机事件的概率,解题的关键是必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,难度适中.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
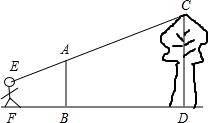 如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
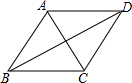 如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )| A. | △ABD与△ABC的周长相等 | |
| B. | 菱形的周长等于两条对角线长之和的两倍 | |
| C. | △ABD与△ADC的周长相等 | |
| D. | 菱形的面积等于两条对角线长之积的两分之一 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | c<b<a | D. | a>c>b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 5$\sqrt{3}$-2$\sqrt{2}$=3$\sqrt{3}$ | D. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com