
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌВЂЭъГЩЯргІЕФШЮЮёЃЎ
ЙХЯЃРАЕФМИКЮбЇМвКЃТздкЫћЕФжјзїЁЖЖШСПТлЁЗвЛЪщжаИјГіСЫРћгУШ§НЧаЮШ§БпжЎГЄЧѓУцЛ§ЕФЙЋЪНЉЉЉЉКЃТзЙЋЪНSЃН![]() ЃЈЦфжаaЃЌbЃЌcЪЧШ§НЧаЮЕФШ§БпГЄЃЌ
ЃЈЦфжаaЃЌbЃЌcЪЧШ§НЧаЮЕФШ§БпГЄЃЌ![]() ЃЌSЮЊШ§НЧаЮЕФУцЛ§ЃЉЃЌВЂИјГіСЫжЄУї
ЃЌSЮЊШ§НЧаЮЕФУцЛ§ЃЉЃЌВЂИјГіСЫжЄУї
Р§ШчЃКдкЁїABCжаЃЌaЃН3ЃЌbЃН4ЃЌcЃН5ЃЌФЧУДЫќЕФУцЛ§ПЩвдетбљМЦЫуЃК
ЁпaЃН3ЃЌbЃН4ЃЌcЃН5
Ёр![]() ЃН6
ЃН6
ЁрSЃН![]() ЃН
ЃН![]() ЃН6
ЃН6
ЪТЪЕЩЯЃЌЖдгквбжЊШ§НЧаЮЕФШ§БпГЄЧѓШ§НЧаЮУцЛ§ЕФЮЪЬтЃЌЛЙПЩгУЮвЙњФЯЫЮЪБЦкЪ§бЇМвЧиОХЩиЬсГіЕФЧиОХЩиЙЋЪНЕШЗНЗЈНтОіЃЎ
ИљОнЩЯЪіВФСЯЃЌНтД№ЯТСаЮЪЬтЃК
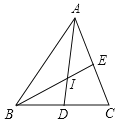
ШчЭМЃЌдкЁїABCжаЃЌBCЃН7ЃЌACЃН8ЃЌABЃН9
ЃЈ1ЃЉгУКЃТзЙЋЪНЧѓЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉШчЭМЃЌADЁЂBEЮЊЁїABCЕФСНЬѕНЧЦНЗжЯпЃЌЫќУЧЕФНЛЕуЮЊIЃЌЧѓЁїABIЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉАДееВФСЯИјГіЕФЙЋЪНЃЌНЋЪ§жЕДњШыМДПЩЧѓГіУцЛ§ЃЛ
ЃЈ2ЃЉЙ§ЕуIзїIFЁЭABЁЂIGЁЭACЁЂIHЁЭBCЃЌДЙзуЗжБ№ЮЊЕуFЁЂGЁЂHЃЌРћгУНЧЦНЗжЯпЕФаджЪПЩжЊIFЃНIHЃНIGЃЌРћгУЕкЃЈ1ЃЉЮЪжаЧѓГіЕФУцЛ§ЧѓГіIFЃЌзюКѓРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓЁїABIЕФУцЛ§МДПЩ.
НтЃКЃЈ1ЃЉЁпBCЃН7ЃЌACЃН8ЃЌABЃН9ЃЌ
Ёр![]()
![]()
Д№ЃКЁїABCУцЛ§ЪЧ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуIзїIFЁЭABЁЂIGЁЭACЁЂIHЁЭBCЃЌДЙзуЗжБ№ЮЊЕуFЁЂGЁЂHЃЌ
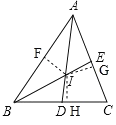
ЁпADЁЂBEЗжБ№ЮЊЁїABCЕФНЧЦНЗжЯпЃЌ
ЁрIFЃНIHЃНIGЃЌ
ЁпSЁїABCЃНSЁїABI+SЁїACI+SЁїBCIЃЌ
Ёр![]() ЃЈ9IF+8IF+7IFЃЉЃН
ЃЈ9IF+8IF+7IFЃЉЃН![]()
НтЕУIFЃН![]()
ЙЪSЁїABIЃН![]() ABFIЃН
ABFIЃН![]() ЁС9ЁС
ЁС9ЁС![]() ЃН
ЃН![]() ЃЎ
ЃЎ


 АйФъбЇЕфПЮЪБбЇСЗВтЯЕСаД№АИ
АйФъбЇЕфПЮЪБбЇСЗВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЬНОПЃЉгУЁАЃОЁБЁЂЁАЃМЁБЁЂЁАЁмЁБЁЂЁАЁнЁБЛђЁАЃНЁБЬюПеЃЌВЂЬНОПЙцТЩЃК
ЃЈ1ЃЉ4+5ЁЁ ЁЁ2![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ3+![]() ЁЁ ЁЁ2
ЁЁ ЁЁ2![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ1+![]() ЁЁ ЁЁ2
ЁЁ ЁЁ2![]() ЃЛ
ЃЛ
ЃЈ4ЃЉa+1ЁЁ ЁЁ2![]() ЃЈaЃО0ЃЉЃЎ
ЃЈaЃО0ЃЉЃЎ
ЃЈЗЂЯжЃЉгУвЛОфЛАИХРЈФуЗЂЯжЕФЙцТЩЃКЁЁ ЁЁЃЛ
ЃЈБэДяЃЉгУЗћКХгябдаДГіФуЗЂЯжЕФЙцТЩВЂМгвджЄУїЃЛ
ЃЈгІгУЃЉШєaЃО0ЃЌЧѓa+![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇПЮЩЯЃЌРЯЪІвЊЧѓдквЛИівбжЊЕФ![]() жаЃЌРћгУГпЙцзїГівЛИіСтаЮ.
жаЃЌРћгУГпЙцзїГівЛИіСтаЮ.
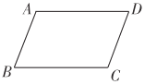
ЃЈ1ЃЉаЁУїЕФзїЗЈШчЯТЃКШчЭМ1ЃЌСЌНг![]() ЃЌзї
ЃЌзї![]() ЕФДЙжБЦНЗжЯп
ЕФДЙжБЦНЗжЯп![]() ЗжБ№НЛ
ЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() .ЧыФуХаЖЯаЁУїЕФзїЗЈЪЧЗёе§ШЗЃЛШєе§ШЗЃЌЫЕУїРэгЩЃЛШєВЛе§ШЗЃЌЧыФузїГіЗћКЯЬѕМўЕФСтаЮЃЛ
.ЧыФуХаЖЯаЁУїЕФзїЗЈЪЧЗёе§ШЗЃЛШєе§ШЗЃЌЫЕУїРэгЩЃЛШєВЛе§ШЗЃЌЧыФузїГіЗћКЯЬѕМўЕФСтаЮЃЛ

ЃЈ2ЃЉаЁССЕФзїЗЈЃКШчЭМ2ЃЌЗжБ№зї![]() ЃЌ
ЃЌ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() ЃЌ
ЃЌ![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЪЧСтаЮ.ЧыФужБНгХаЖЯаЁССЕФзїЗЈЪЧЗёе§ШЗ.
ЪЧСтаЮ.ЧыФужБНгХаЖЯаЁССЕФзїЗЈЪЧЗёе§ШЗ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
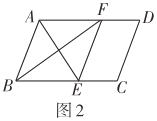
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЌСЌНг
ЕФЧаЯпЃЌСЌНг![]() НЛ
НЛ![]() гкEЃЌЙ§ЕуAзї
гкEЃЌЙ§ЕуAзї![]() гкFЃЌНЛ
гкFЃЌНЛ![]() гкDЃЌСЌНг
гкDЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
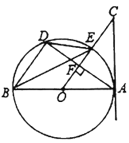
ЁОЬтФПЁПШчЭМЃЌвдADЮЊжБОЖЕФАыдВOОЙ§RtЁїABCаББпABЕФСНИіЖЫЕуЃЌНЛжБНЧБпACгкЕуEЃЛBЁЂEЪЧАыдВЛЁЕФШ§ЕШЗжЕуЃЌ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
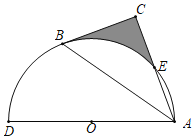
ЁОЬтФПЁПШчЭМЃЌдкШёНЧШ§НЧаЮABCжаЃЌЕуDЃЌEЗжБ№дкБпACЃЌABЩЯЃЌAGЁЭBCгкЕуGЃЌAFЁЭDEгкЕуFЃЌЁЯEAF=ЁЯGACЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁзЁїABCЃЛ
ЃЈ2ЃЉШєAD=3ЃЌAB=5ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаДйЯњЛюЖЏЃЌНЋAЃЌBЃЌCШ§жжЫЎЙћВЩгУМзЁЂввЁЂБћШ§жжЗНЪНДюХфзАНјРёКаНјааЯњЪлЃЎУПКаЕФзмГЩБОЮЊКажаAЃЌBЃЌCШ§жжЫЎЙћГЩБОжЎКЭЃЌКазгГЩБОКіТдВЛМЦЃЎМзжжЗНЪНУПКаЗжБ№зАAЃЌBЃЌCШ§жжЫЎЙћ6kgЃЌ3kgЃЌ1kgЃЛввжжЗНЪНУПКаЗжБ№зАAЃЌBЃЌCШ§жжЫЎЙћ2kgЃЌ6kgЃЌ2kgЃЎМзУПКаЕФзмГЩБОЪЧУПЧЇПЫAЫЎЙћГЩБОЕФ12.5БЖЃЌУПКаМзЕФЯњЪлРћШѓТЪЮЊ20%ЃЛУПКаМзБШУПКаввЕФЪлМлЕЭ25%ЃЛУПКаБћдкГЩБОЩЯЬсИп40%БъМлКѓДђАЫелГіЪлЃЌЛёРћЮЊУПЧЇПЫAЫЎЙћГЩБОЕФ1.2БЖЃЎЕБЯњЪлМзЁЂввЁЂБћШ§жжЗНЪНДюХфЕФРёКаЪ§СПжЎБШЮЊ2ЃК2ЃК5ЪБЃЌдђЯњЪлзмРћШѓТЪЮЊ_____ЃЎЃЈРћШѓТЪЃНРћШѓЁТГЩБОЁС100%ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
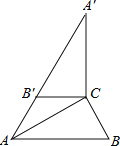
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯBЃН60ЁуЃЌBCЃН2ЃЎНЋЁїABCШЦЕуCЫГЪБеыа§зЊЃЌЕУЕНЁїAЁфBЁфCЃЌСЌНгABЁфЃЌЧвAЃЌBЁфЃЌAЁфдкЭЌвЛЬѕжБЯпЩЯЃЌдђAAЁфЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌНЋЁїABCШЦЖЅЕуCФцЪБеыа§зЊЕУЕНЁїAЁфBЁфCЃЌMЪЧBCЕФжаЕуЃЌPЪЧAЁфBЁфЕФжаЕуЃЌСЌНгPMЃЌШєBCЃН2ЃЌЁЯBACЃН30ЁуЃЌдђЯпЖЮPMЕФзюДѓжЕЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com