练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在一个不透明的袋子中有20个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中红球的个数约为（　　）

    　  A． 4             B． 6                 C． 8                D． 12


    C

        解：由题意可得：，

    解得：x=8，


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，已知直线m∥m，∠1=100°，则∠2的度数为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：1﹣（﹣）=（　　）

    　  A．            B． ﹣             C．                D． ﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：÷﹣，其中m=﹣3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


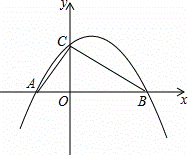
    如图，已知抛物线y=ax2+bx+c经过A（﹣2，0），B（4，0），C（0，3）三点．

    （1）求该抛物线的解析式；

    （2）在y轴上是否存在点M，使△ACM为等腰三角形？若存在，请直接写出所有满足要求的点M的坐标；若不存在，请说明理由；

    （3）若点P（t，0）为线段AB上一动点（不与A，B重合），过P作y轴的平行线，记该直线右侧与△ABC围成的图形面积为S，试确定S与t的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，从一块半径是1m的圆形铁皮（⊙O）上剪出一个圆心角为60°的扇形（点A，B，C在⊙O上），将剪下的扇形围成一个圆锥，则这个圆锥的底面圆的半径是（　　）

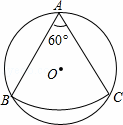
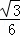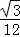    　  A． m          B． m              C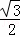． m              D． 1m

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：（﹣2）3+3tan45°﹣．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，直线AB与x轴交于点A（﹣2，0），与x轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线y=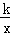（k≠0）上，则k的值为（　　）

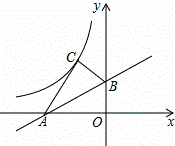
    　 A． 4 B． ﹣2 C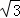．  D． ﹣

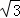
    查看答案和解析>>

    科目：初中数学 来源： 题型：


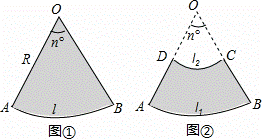
    如图①，半径为R，圆心角为n°的扇形面积是S扇形=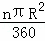，由弧长l=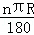，得S扇形=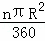=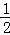••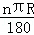R=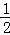lR．通过观察，我们发现S扇形=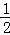lR类似于S三角形=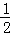×底×高．

    类比扇形，我们探索扇环（如图②，两个同心圆围成的圆环被扇形截得的一部分交作扇环）的面积公式及其应用．

    （1）设扇环的面积为S扇环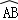，的长为l1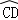，的长为l2，线段AD的长为h（即两个同心圆半径R与r的差）．类比S梯形=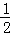×（上底+下底）×高，用含l1，l2，h的代数式表示S扇环，并证明；

    （2）用一段长为40m的篱笆围成一个如图②所示的扇环形花园，线段AD的长h为多少时，花园的面积最大，最大面积是多少？

    查看答案和解析>>

    同步练习册答案