
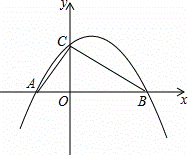
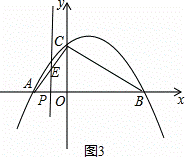
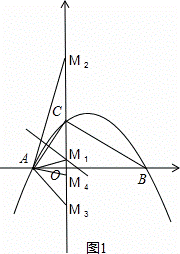
如图,已知抛物线y=ax2+bx+c经过A(﹣2,0),B(4,0),C(0,3)三点.
(1)求该抛物线的解析式;
(2)在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;
(3)若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.
解:(1)把A(﹣2,0),B(4,0),C(0,3)代入抛物线y=ax2+bx+c得:
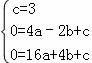
 ,
,
解得: ,
,
则抛物线的解析式是:y=﹣ x2+
x2+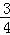 x+3;
x+3;
(2)如图1,作线段CA的垂直平分线,交y轴于M,交AC与N,连结AM1,则△AM1C是等腰三角形,
∵AC= =
=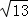 ,
,
∴CN=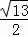 ,
,
∵△CNM1∽△COA,
∴ =
= ,
,
∴ =
=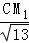 ,
,
∴CM1=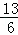 ,
,
∴OM1=OC﹣CM1=3﹣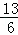 =
=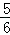 ,
,
∴M1的坐标是(0,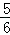 ),
),
当CA=CM2=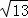 时,则△AM2C是等腰三角形,
时,则△AM2C是等腰三角形,
则OM2=3+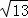 ,
,
M2的坐标是(0,3+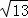 ),
),
当CA=AM3= 时,则△AM3C是等腰三角形,
时,则△AM3C是等腰三角形,
则OM3=3,
M3的坐标是(0,﹣3),
当CA=CM4= 时,则△AM4C是等腰三角形,
时,则△AM4C是等腰三角形,
则OM4= ﹣3,
﹣3,
M4的坐标是(0,3﹣ ),
),
(3)如图2,当点P在y轴或y轴右侧时,
设直线与BC交与点D,
∵OB=4,OC=3,
∴S△BOC=6,
∵BP=BO﹣OP=4﹣t,
∴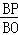 =
= ,
,
∵△BPD∽△BOC,
∴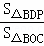 =(
=( )2,
)2,
∴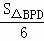 =(
=(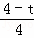 )2,
)2,
∴S=S△BPD=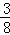 t2﹣3t+6(0≤t<4);
t2﹣3t+6(0≤t<4);
当点P在y轴左侧时,
设直线与AC交与点E,
∵OP=﹣t,AP=t+2,
∴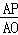 =
=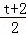 ,
,
∵ =(
=( )2,
)2,
∴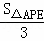 =(
=( )2,
)2,
∴S△APE= ,
,
∴S=S△ABC﹣S△APE=9﹣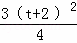 =﹣
=﹣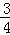 t2﹣3t+6(﹣2<t<0).
t2﹣3t+6(﹣2<t<0).



 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=3,将△ABD沿对角线BD对折,得到△EBD,DE与BC交于点F,∠ADB=30°,则EF=( )

A.  B. 2
B. 2 C. 3 D. 3
C. 3 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
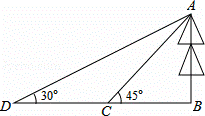
一数学兴趣小组为了测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得A的仰角为30°,求树高.(结果精确到0.1米,参考数据: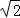 ≈1.414,
≈1.414,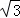 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的袋子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中红球的个数约为( )
A. 4 B. 6 C. 8 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
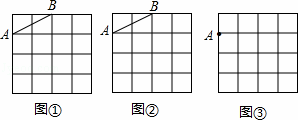
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com