
(本题12分)如图,抛物线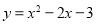 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.

(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,连接EA,EC,求△ACE面积最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由.
(1)A(-1,0),B(3,0),直线AC的函数表达式为y=-x-1;(2)S△AEC 的最大值为 ;(3)F1(1,0),F2(-3,0),F3(4+
;(3)F1(1,0),F2(-3,0),F3(4+ ,0),F4(4-
,0),F4(4- ,0).
,0).
【解析】
试题分析:(1) ,令y=0,得
,令y=0,得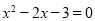 ,解方程可得点AB的横坐标,从而可得A(-1,0),B(3,0),将C点的横坐标为2代入
,解方程可得点AB的横坐标,从而可得A(-1,0),B(3,0),将C点的横坐标为2代入 .可得点C的坐标,然后设直线AC的函数解析式为
.可得点C的坐标,然后设直线AC的函数解析式为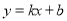 ,将A(-1,0), C(2,-3)代入,可得直线AC解析式;(2)设P点的横坐标为x(-1≤x≤2),根据条件可表示出P、E的坐标以及线段PE的长,然后根据三角形的面积公式可表示出△ACE面积,将关系式配方可解;(3)观察图形找出所有可能的情况,利用平行四边形的性质分情况解答.
,将A(-1,0), C(2,-3)代入,可得直线AC解析式;(2)设P点的横坐标为x(-1≤x≤2),根据条件可表示出P、E的坐标以及线段PE的长,然后根据三角形的面积公式可表示出△ACE面积,将关系式配方可解;(3)观察图形找出所有可能的情况,利用平行四边形的性质分情况解答.
试题解析:【解析】
(1)令y=0,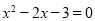 ,解得x=-1或x=3,
,解得x=-1或x=3,
∴A(-1,0),B(3,0),
将C点的横坐标x=2,代入 ,得:y=-3,∴C(2,-3);
,得:y=-3,∴C(2,-3);
设直线AC的函数解析式为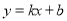 ,将A(-1,0), C(2,-3)代入,
,将A(-1,0), C(2,-3)代入,
得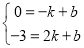 ,解得
,解得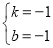 ,∴直线AC的函数表达式为y=-x-1.
,∴直线AC的函数表达式为y=-x-1.
(2)设P点的横坐标为x(-1≤x≤2),
则P、E的坐标分别为:P(x,-x-1),E(x,x2-2x-3),
∴PE=(-x-1)-(x2-2x-3)=-x2+x+2=-(x-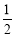 )2+
)2+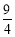 ,
,
∴S△AEC=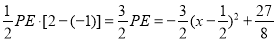 ,
,
∴当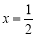 时,S△AEC 的最大值为
时,S△AEC 的最大值为 ;----8分
;----8分
(3)存在4个这样的点F,分别是:F1(1,0),F2(-3,0),F3(4+ ,0),F4(4-
,0),F4(4- ,0).(每写对一个得1分)
,0).(每写对一个得1分)
参考解答如下:
①如图1,连接C与抛物线和y轴的交点G,那么CG∥x轴,当AF=CG=2时,此时四边形ACGF为平行四边形,因此F点的坐标是(﹣3,0);
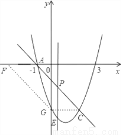
图1
②如图2,AF=CG=2,此时四边形AGCF为平行四边形,因此F点的坐标为(1,0);
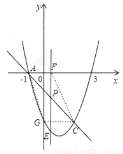
图2
③如图3,
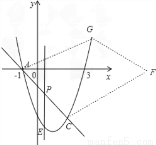

图3
设F(x,0), 当四边形ACFG为平行四边形时,可求得G(x-3,3),代入抛物线 ,得
,得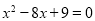 ,
,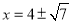 ,因此F点的坐标为(4+
,因此F点的坐标为(4+ ,0)或(4-
,0)或(4- ,0).
,0).
考点:1.待定系数法求函数解析式;2.二次函数的性质;3. 平行四边形的性质;4.分类讨论思想.


科目:初中数学 来源: 题型:
某种商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少时每个月可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求y与x的函数关系式;
(2)问销售该商品第几天时,每天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4 800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市八年级上学期期末考试数学试卷(解析版) 题型:选择题
已知,一次函数y=kx+b的图象如图所示,下列结论正确的是( ).
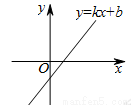
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市八年级上学期期末考试数学试卷(解析版) 题型:选择题
以下列长度的三条线段为边,不能组成直角三角形的是( ).
A.3,4,5 B.6,8,10 C.5,12,13 D.1,1,2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级下学期期始考试数学试卷(解析版) 题型:解答题
(本题8分)某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
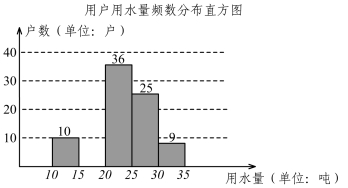
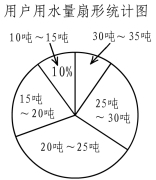
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级下学期期始考试数学试卷(解析版) 题型:填空题
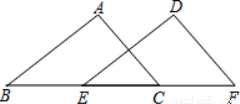
如图,△DEF是由△ABC通过平移得到,且点B,E,C,F在同一条直线上.若BF=14,EC=6.则BE的长度是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省高密市九年级下学期开学考试数学试卷(解析版) 题型:解答题
(本题满分12分).某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福鼎市九年级上学期期中考试数学试卷(解析版) 题型:填空题
某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,若设平均每月增长的百
分率为x,根据题意可列出的方程为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com