
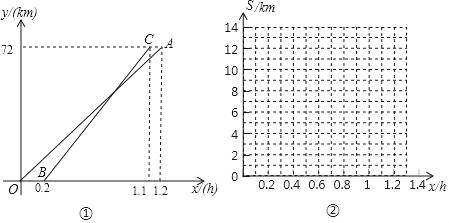
【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图象.
(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)当x为多少时,两人相距6km?
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图象.
【答案】(1)线段OA的函数表达式为y1=60x(0≤x≤1.2).线段BC的函数表达式为y2=80x﹣16(0.2≤x≤1.1).(2)x为0.5或1.1时,两人相距6km.(3)图象见解析.
【解析】试题分析:(1)根据待定系数法可求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)分3种情况:①0<x<0.2;②甲、乙两人相遇前;③甲、乙两人相遇后;进行讨论可求x的值;
(3)分4种情况:①0<x<0.2;②甲、乙两人相遇前;③甲、乙两人相遇后乙到达景点前;④甲、乙两人相遇后乙到达景点后;进行讨论可画出S关于x的函数图象.
【解答】解:(1)设OA:y1=k1x,BC:y2=k2x+b,
则y1=k1x过点(1.2,72),
所以y1=60x,
∵y2=k2x+b过点(0.2,0)、(1.1,72),
∴![]()
解得![]() .
.
∴y2=80x-16.
(2)①60x=6,
解得x=0.1;
②60x-(80x-16)=6,
解得x=0.5;
③80x-16-60x=6,
解得x=1.1.
故当x为0.1或0.5或1.1小时,两人相距6千米.
(3)如图所示: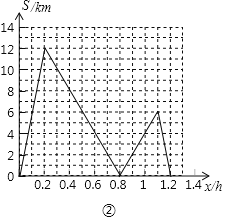


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
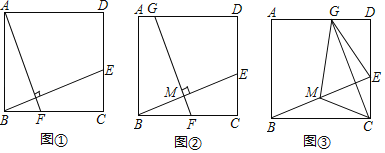
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,∠1+∠2=230°,b∥c,则∠1,∠2,∠3,∠4各是多少度?
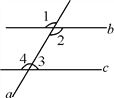
解:∵∠1=∠2(__________________),
∠1+∠2=230°,
∴∠1=∠2=___________(填度数).
∵b∥c,
∴∠4=∠2=_______(填度数)(_______________________________),
∠2+∠3=180°(________________________________),
∴∠3=180°-∠2=____________(填度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师从咸宁出发到外地参加教育信息化应用技术提高培训,他可以乘坐普通列车,也可以乘坐高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍.若高铁的平均速度(千米/小时)是普通列车平均速度的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
已知:如图1,![]() ,
,![]() .求证:
.求证:![]() .
.

老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的
,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的![]() 、
、![]() 与
与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图2中![]() 、
、![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
②补全图4,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
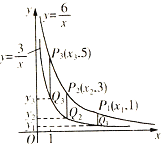
【题目】两个反比例函数![]() ,
,![]() 在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数![]() 图象上,它们的横坐标分别是x1,x2,x3,x2005纵坐标分别为1,3,5,……;
图象上,它们的横坐标分别是x1,x2,x3,x2005纵坐标分别为1,3,5,……;
共2005个连续奇数,过点P1,P2,P3,……,P2005分别作![]() 轴的平行线,与
轴的平行线,与![]() 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2005(x2005,y2005),则
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2005(x2005,y2005),则![]() _____________.
_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)( )
≈1.732)( )
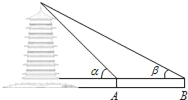
A. 36.21米 B. 37.71米 C. 40.98米 D. 42.48米
查看答案和解析>>
科目:初中数学 来源: 题型:
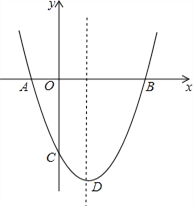
【题目】如图,抛物线![]() 与y轴交于点
与y轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点D为抛物线的顶点.
,点D为抛物线的顶点.
![]() 求抛物线解析式和顶点D的坐标;
求抛物线解析式和顶点D的坐标;
![]() 求抛物线与x轴的两交点A、B的坐标;
求抛物线与x轴的两交点A、B的坐标;
![]() 你可以直接写出不等式
你可以直接写出不等式![]() 的解集吗?
的解集吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com