
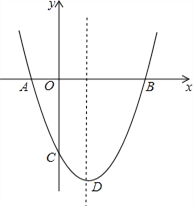
【题目】如图,抛物线![]() 与y轴交于点
与y轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点D为抛物线的顶点.
,点D为抛物线的顶点.
![]() 求抛物线解析式和顶点D的坐标;
求抛物线解析式和顶点D的坐标;
![]() 求抛物线与x轴的两交点A、B的坐标;
求抛物线与x轴的两交点A、B的坐标;
![]() 你可以直接写出不等式
你可以直接写出不等式![]() 的解集吗?
的解集吗?
【答案】(1)顶点D的坐标为![]() ;(2)
;(2)![]() 、B的坐标分别为
、B的坐标分别为![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)把点C(0,-3)代入解析式可得c=-3,由对称轴为直线x=![]() 可解得b=-2,由此即可得到抛物线的解析式;再把所得解析式配方化为“顶点式”,即可得到顶点坐标;
可解得b=-2,由此即可得到抛物线的解析式;再把所得解析式配方化为“顶点式”,即可得到顶点坐标;
(2)由二次函数解析式中y=0,解得对应的x的值,即可求得A、B两点的坐标;
(3)由(2)中所求A、B的坐标结合抛物线开口向上即可得到不等式![]() 的解集.
的解集.
试题解析:
(1)∵抛物线![]() 与y轴交于点
与y轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,
∴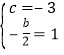 ,解得:b=-2,c=3,
,解得:b=-2,c=3,
∴抛物线的解析式为:y=x2-2x-3,
∵y=x2-2x+3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4);
(2)在y=x2-2x-3中,当y=0时,x2-2x-3=0,解得:x1=3,x2=-1,
∴A的坐标为(-1,0),B的坐标为(3,0);
(3)∵A的坐标为(-1,0),B的坐标为(3,0),抛物线y=x2-2x-3开口向上,
∴![]() 的解集为:
的解集为:![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
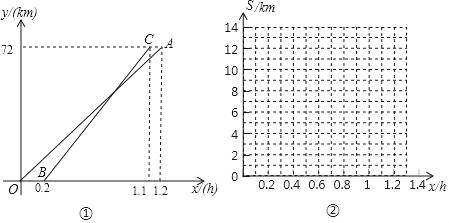
【题目】甲、乙两人周末从同一地点出发去某景点,因乙临时有事,甲坐地铁先出发,甲出发0.2小时后乙开汽车前往.设甲行驶的时间为x(h),甲、乙两人行驶的路程分别为y1(km)与y2(km).如图①是y1与y2关于x的函数图象.
(1)分别求线段OA与线段BC所表示的y1与y2关于x的函数表达式;
(2)当x为多少时,两人相距6km?
(3)设两人相距S千米,在图②所给的直角坐标系中画出S关于x的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
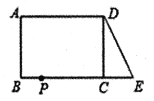
【题目】已知:如图,在长方形![]() 中,
中,![]() ,
,![]() .延长
.延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿
出发,以每秒2个单位的速度沿![]() 向终点
向终点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒,当
秒,当![]() 的值为___________时,
的值为___________时,![]() 和
和![]() 全等.
全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
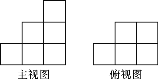
【题目】由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如图29-29所示.
(1)请你画出这个几何体的一种左视图.
(2)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交于两点A、
与x轴交于两点A、![]() 点A在x轴的正半轴上,点B在x轴的负半轴上
点A在x轴的正半轴上,点B在x轴的负半轴上![]() 与y轴交于点C.
与y轴交于点C.
![]() 求m的取值范围;
求m的取值范围;
![]() 如果
如果![]() :
:![]() :1,在该抛物线对称轴右边图象上求一点P的坐标,使得
:1,在该抛物线对称轴右边图象上求一点P的坐标,使得![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
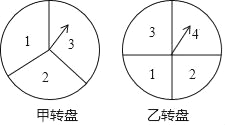
【题目】如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)转动甲转盘,指针指向的数字小于3的概率是 ;
(2)同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com