
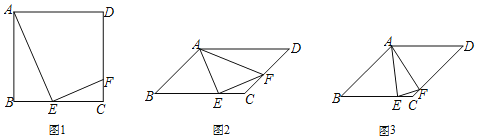
【题目】如图1,在正方形ABCD中,E是边BC的中点,F是CD上一点,已知∠AEF=90°.
(1)求证:![]() ;
;
(2)平行四边形ABCD中,E是边BC上一点,F是边CD上一点,∠AFE=∠ADC,∠AEF=90°.
①如图2,若∠AFE=45°,求![]() 的值;
的值;
②如图3,若AB=BC,EC=3CF,直接写出cos∠AFE的值.
【答案】(1)见解析;(2)①![]() ;②cos∠AFE=
;②cos∠AFE=![]()
【解析】
(1)用特殊值法,设![]() ,则
,则![]() ,证
,证![]() ,可求出CF,DF的长,即可求出结论;
,可求出CF,DF的长,即可求出结论;
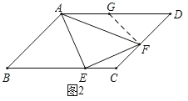
(2)①如图2,过F作![]() 交AD于点G,证
交AD于点G,证![]() 和
和![]() 是等腰直角三角形,证
是等腰直角三角形,证![]() ,求出
,求出![]() 的值,即可写出
的值,即可写出![]() 的值;②如图3,作
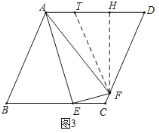
的值;②如图3,作![]() 交AD于点T,作
交AD于点T,作![]() 于H,证
于H,证![]() ,设CF=2,则CE=6,可设AT=x,则TF=3x,
,设CF=2,则CE=6,可设AT=x,则TF=3x,![]() ,
,![]() ,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
,分别用含x的代数式表示出∠AFE和∠D的余弦值,列出方程,求出x的值,即可求出结论.
(1)设BE=EC=2,则AB=BC=4,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠FEC=∠EAB,
又∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴CF=1,
则![]() ,
,
∴![]() ;
;
(2)①如图2,过F作![]() 交AD于点G,
交AD于点G,
∵![]() ,
,
∴![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴∠AGF=∠C,
又∵![]() ,
,
∴∠GAF=∠CFE,
∴![]() ,
,
∴![]() ,
,
又∵GF=DF,
∴![]() ;
;
②如图3,作![]() 交AD于点T,作
交AD于点T,作![]() 于H,
于H,
则![]() ,
,
∴![]() ,
,
∴∠ATF=∠C,
又∵![]() ,且∠D=∠AFE,
,且∠D=∠AFE,
∴∠TAF=∠CFE,
∴![]() ,
,
∴![]() ,
,
设CF=2,则CE=6,可设AT=x,则TF=3x,![]() ,
,
∴![]() ,且
,且![]() ,
,
由![]() ,得
,得![]() ,
,
解得x=5,
∴![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
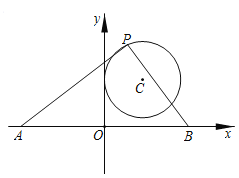
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是上海世博园内的一个矩形花园,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
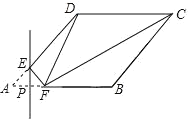
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=2,P为线段AB上一动点,且不与点A重合,过点P作PE⊥AB交AD于点E,将∠A沿PE折叠,点A落在直线AB上点F处,连接DF、CF,当△CDF为等腰三角形时,AP的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为![]() 的三角形面积。
的三角形面积。
问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为![]() 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB=![]() 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=![]() 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC=![]() 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
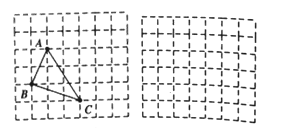
(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为![]() 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
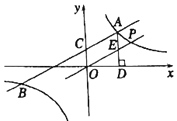
【题目】如图,一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com