
【题目】如图,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC交于点E. 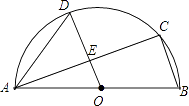
(1)若∠B=80°,求∠CAD的度数;
(2)若AB=8,AC=6,求DE的长.
【答案】
(1)解:∵OD∥BC,
∴∠AOD=∠B=80°,
∴∠OAD=∠ODA=50°,
∵AB是半圆O的直径,
∴∠C=90°,
∴∠CAB=10°,
∴∠CAD=50°﹣10°=40°
(2)解:∵∠C=90°,AB=8,AC=6,
∴BC= ![]() =2
=2 ![]() ,
,
∵OD∥BC,OA=OB,
∴OE= ![]() BC=
BC= ![]() ,
,
∴DE=4﹣ ![]()
【解析】(1)根据平行线的性质求出∠AOD,根据等腰三角形的性质求出∠OAD,根据圆周角定理求出∠CAB,计算即可;(2)根据勾股定理求出BC,根据三角形中位线定理求出OE,结合图形计算.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系. 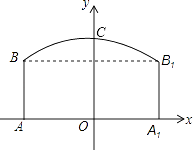
(1)求该抛物线的函数表达式,并求出自变量x的取值范围;
(2)一大型货运汽车装载大型设备后高为6m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )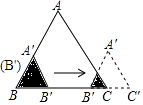
A.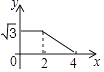
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(﹣1,0),C(0,﹣5)两点,与x轴交于点B.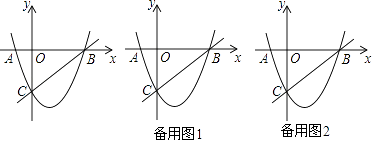
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q?若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么下列结论: ①a<0,②b<0,③c<0,
其中正确的判断是( )
A.①②
B.①③
C.②③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号) 根据以上信息,解答下列问题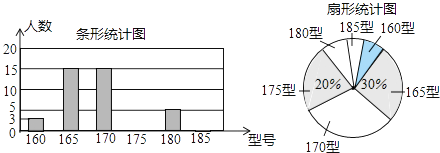
(1)该班共有多少名学生,其中穿175型号校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整;
(3)在扇形统计图中,请计算185型号校服所对应的扇形圆心角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE= ![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF . 正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF . 正确的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com