
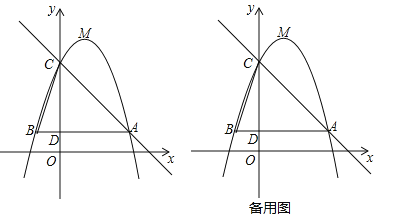
����Ŀ����ͼ����֪���κ���![]() ��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��b��cΪ��������ͼ����A��3��1������C��0��4��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ������ڡ�ABC���ڲ�����������ABC�ı߽磩����m��ȡֵ��Χ��
��3����P��ֱ��AC�ϵĶ��㣬����P����C����M�����ɵ����������BCD���ƣ���ֱ��д�����е�P�����ֱ꣨��д�����������д�����̣���
���𰸡���1��![]() ��M��1��5������2��2��m��4����3��P1��
��M��1��5������2��2��m��4����3��P1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����
����������1���ѵ�A��3��1������C��0��4��������κ���![]() ������
������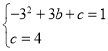 �����
�����![]() �������κ�������ʽΪ
�������κ�������ʽΪ![]() ���䷽��
���䷽��![]() ������M������Ϊ��1��5����
������M��������1��5����
��2����ֱ��AC����ʽΪy=kx+b���ѵ�A��3��1����C��0��4���������![]() �����
�����![]() ����ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F��
����ֱ��AC�Ľ���ʽΪy=��x+4����ͼ��ʾ���Գ���ֱ��x=1���ABC���߷ֱ��ڵ�E����F��
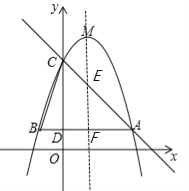
��x=1����ֱ��AC����ʽy=��x+4���y=3�����E����Ϊ��1��3������F����Ϊ��1��1������1��5��m��3�����2��m��4��
��3������MC����MG��y�Ტ�ӳ���AC�ڵ�N�����G����Ϊ��0��5����
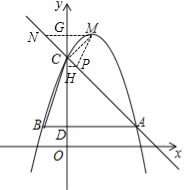
��MG=1��GC=5��4=1����MC=![]() =
=![]() =
=![]() ����y=5����y=��x+4���x=��1�����N����Ϊ����1��5������NG=GC��GM=GC������NCG=��GCM=45�㣬����NCM=90�㣬�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ����
����y=5����y=��x+4���x=��1�����N����Ϊ����1��5������NG=GC��GM=GC������NCG=��GCM=45�㣬����NCM=90�㣬�ɴ˿�֪������P��AC�ϣ����MCP=90�㣬���D���C��Ϊ���������ζ�Ӧ����
�����С�PCM�ס�BDC������![]() ����BD=1��CD=3����CP=
����BD=1��CD=3����CP=![]() =
=![]() =
=![]() ����CD=DA=3������DCA=45�㣬����P��y���Ҳ࣬��PH��y�ᣬ����PCH=45�㣬CP=
����CD=DA=3������DCA=45�㣬����P��y���Ҳ࣬��PH��y�ᣬ����PCH=45�㣬CP=![]() ����PH=
����PH=![]() =
=![]() ����x=
����x=![]() ����y=��x+4�����y=
����y=��x+4�����y=![]() ����P1��
����P1��![]() ��
��![]() ����
����
ͬ���ɵã�����P��y����࣬���x=![]() ����y=��x+4�����y=
����y=��x+4�����y=![]() ����P2��
����P2��![]() ��
��![]() ����
����
�����С�PCM�ס�CDB������![]() ����CP=
����CP=![]() =
=![]() ����PH=
����PH=![]() =3��
=3��
����P��y���Ҳ࣬��x=3����y=��x+4�����y=1��
����P��y����࣬��x=��3����y=��x+4�����y=7
��P3��3��1����P4����3��7���������з�������õ�P������4�����ֱ�ΪP1��![]() ��
��![]() ����P2��
����P2��![]() ��
��![]() ����P3��3��1����P4����3��7����
����P3��3��1����P4����3��7����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�5��1�վ��д����Żݻ�����쵽���̵깺����Ʒ�����ַ���������һ����168Ԫ�����Ա����Ϊ��Ա��ƾ��Ա�������̵����κ���Ʒ��һ�ɰ���Ʒ�۸��8���Żݣ������������������Ա���������̵����κ���Ʒһ�ɰ���Ʒ�۸��9.5���Ż�.
��1����С���������Ա������������Ʒ�ļ۸�Ϊ120Ԫʱ��ʵ��Ӧ֧������Ԫ��
��2�����С����һ�㣬��������Ʒ�ļ۸�Ϊ����Ԫʱ�������������������ͬ��
��3��������Ʒ�ļ۸�Ԫʱ�����÷���һ�����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ�����Σ���A������Ϊ��0��2������B������Ϊ��0����3�������������� ![]() ��ͼ����C��һ�κ���y=ax+b��ͼ����A��C��
��ͼ����C��һ�κ���y=ax+b��ͼ����A��C��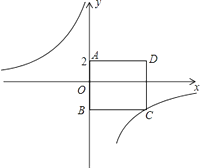
��1������������һ�κ����Ľ���ʽ��
��2������P�Ƿ���������ͼ���ϵ�һ�㣬��OAP�����ǡ�õ���������ABCD���������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������г��IJ���ʽ�У���ȷ����(����)
A. a���Ǹ������ɱ�ʾ��a��0 B. x������3���ɱ�ʾ��x��3
C. m��4�IJ��Ǹ������ɱ�ʾ��m��4��0 D. x��2�ĺ��ǷǸ������ɱ�ʾ��x��2��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=mx+5��ͼ����A��1��4����B��n �� 2��.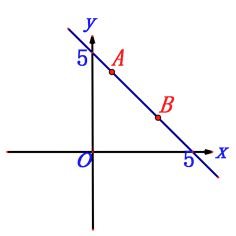
��1����m��n��ֵ��
��2��������ͼ���ڵ�һ����ʱ���Ա���x��ȡֵ��Χ��ʲô��
��3����x������һ��P��ʹPA+PB��̡������P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm����BAC=60�㣬����M�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����N�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
��1����BM=BN����t��ֵ��
��2������MBN���ABC���ƣ���t��ֵ��
��3����tΪ��ֵʱ���ı���ACNM�������С���������Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�꼶��֯ѧ���μ�����Ӫ����Ϊ�ס��ҡ���������л����������ͳ��ͼ��ӳ��ѧ�������μ�����Ӫ��������������ͼ�е���Ϣ�ش��������⣺
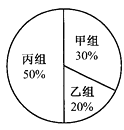
���������ֲ�ֱ��ͼ ������������ͳ��ͼ
��1������꼶�����μӱ��λ����������
��2������꼶�����μ����������������ȫƵ���ֲ�ֱ��ͼ��
��3������ʵ���������Ӽ���������ͬѧ�����飬ʹ���������Ǽ���������3������ô��Ӧ�Ӽ�����������ѧ�������飿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com