
【题目】已知二次函数y=x2﹣(a﹣1)x+a﹣2,其中a是常数. 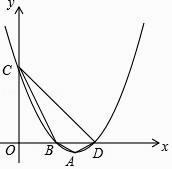
(1)求证:不论a为何值,该二次函数的图象与x轴一定有公共点;
(2)当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积.
【答案】
(1)证明:y=x2﹣(a﹣1)x+a﹣2.
因为[﹣(a﹣1)]2﹣4(a﹣2)=(a﹣3)2≥0.
所以,方程x2﹣(a﹣1)x+a﹣2=0有实数根.
所以,不论a为何值,该函数的图象与x轴总有公共点;
(2)解:由题可知:当a=4时,y=x2﹣3x+2,
因为y=x2﹣3x+2=(x﹣ ![]() )2﹣
)2﹣ ![]() ,所以A(
,所以A( ![]() ,﹣
,﹣ ![]() ),
),
当y=0时,x2﹣3x+2=0,解得x1=1,x2=2,所以B(1,0),D(2,0),
当x=0时,y=2,所以C(0,2),
所以S四边形ABCD=S△ABD+S△BDC= ![]() +1=
+1= ![]() .
.
【解析】(1)利用根的判别式符号进行证明;(2)由抛物线解析式求得点B、C、D的坐标,然后利用分割法来求四边形ABCD的面积.
【考点精析】通过灵活运用抛物线与坐标轴的交点,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.


科目:初中数学 来源: 题型:
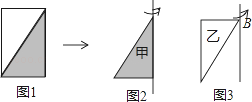
【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】饮水机原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y与开机时间x满足一次函数关系),当加热到100℃是自动停止加热,随后水温开始下降(此过程水温y与开机时间x成反比例关系),当水温将至20℃时,饮水机又自动开始加热,…重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8,求水温y与开机时间x的函数关系.
(2)求图中t的值.
(3)在通电后45分钟饮水机内水温约为多少度?在通电后60分钟饮水机内水温约为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图. 上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a=;b=;
(2)补全频数分布直方图; 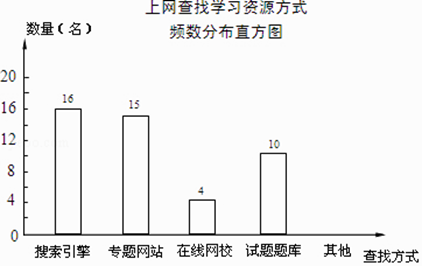
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标有数字﹣2,1,4.随机摸出一个小球(不放回),其数字为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形ABCD中,点A,B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D→A匀速运动,同时动点Q以相同的速度在x轴正半轴上运动,当点P到达A点时,两点同时停止运动,设运动的时间为t秒.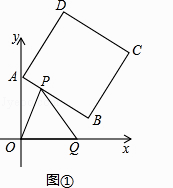
(1)当P点在边AB上运动时点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;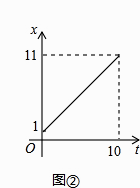
(2)求正方形边长及顶点C的坐标;
(3)在(1)中,设△OPQ的面积为S,求S与t的函数关系式并写出自变量的取值范围.
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等?若能,写出所有符合条件的t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图的调查问卷(单选).在随机调查了某市全部10000名司机中的部分司机后,统计整理并制作了如下的统计图: 
根据以上信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中m=;
(2)该市支持选项C的司机大约有多少人?
(3)若要从该市支持选项C的司机中随机选择200名,给他们签订“永不酒驾”的保证书,则支持该选项的司机小李被选中的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com