
����Ŀ����ˮ��ԭ��ˮ���¶�Ϊ20�棬ͨ�翪������ˮ���Զ���ʼ���ȣ��˹�����ˮ��y�뿪��ʱ��x����һ�κ�����ϵ���������ȵ�100�����Զ�ֹͣ���ȣ����ˮ�¿�ʼ�½����˹���ˮ��y�뿪��ʱ��x�ɷ�������ϵ������ˮ�½���20��ʱ����ˮ�����Զ���ʼ���ȣ����ظ�����������ͼ��ʾ��������ͼ���ṩ����Ϣ������������⣺
��1����0��x��8����ˮ��y�뿪��ʱ��x�ĺ�����ϵ.
��2����ͼ��t��ֵ.
��3����ͨ���45������ˮ����ˮ��ԼΪ���ٶȣ���ͨ���60������ˮ����ˮ��ԼΪ���ٶȣ�

���𰸡���1����������ʽΪ��y=10x+20�� ��2��t=40�� ��3��45����ʱ����ˮ���ڵ��¶�ԼΪ70����60����ʱ����ˮ���ڵ��¶�ԼΪ40��.
��������������
��1���������Ϻ���ͼ������������ϵʽΪy=kx+b�����㣨0��20���͵㣨8��100���������躯����ϵʽ�г������飬�ⷽ�������k��b��ֵ���ɵõ���������ϵʽ��
��2����ˮ���½�������y��x��ĺ�����ϵʽΪ��![]() �����㣨8��100�����������ϵʽ���m��ֵ�����ɵõ�ˮ���½�������y��x��ĺ�����ϵʽΪ
�����㣨8��100�����������ϵʽ���m��ֵ�����ɵõ�ˮ���½�������y��x��ĺ�����ϵʽΪ![]() ���ٽ�y=20�������ú�����ϵʽ�������t=40��
���ٽ�y=20�������ú�����ϵʽ�������t=40��
��3������x=45ʱ����45-t=5<8��֪����ʱ���ڼ��ȽΣ���x=5���루1�������ú�����ϵʽ������ô�ʱ��Ӧ��ˮ�£�����x=60ʱ����60-40=20>8����20<40��֪����ʱ����ˮ���½�������x=20���루2�������ú�����ϵʽ������ô�ʱ��Ӧ��ˮ����.
�����
��1����0��x��8ʱ����ˮ��y���棩�뿪��ʱ��x���֣��ĺ�����ϵΪ��y=kx+b��
�������⣬��![]() ����ã�
����ã�![]() ��
��
������������ʽΪ��y=10x+20��
��2����ˮ���½������У���ˮ��y���棩��
����ʱ��x���֣��ĺ�����ϵʽΪ��![]() ��
��
�������⣬�ã�100=![]() ����m=800����
����m=800����![]() ��
��
��y=20ʱ��20=![]() ����ã�t=40��
����ã�t=40��
��3������45��40=5��8��
��45����ʱ�����ڼ��ȽΣ�
�ߵ�x=5ʱ��y=10��5+20=70��
��45����ʱ����ˮ���ڵ��¶�ԼΪ70����
�ڡ�60��40=20>8����20<40��
��60����ʱ������ˮ���½��Σ�
�ߵ�x=20ʱ��y=![]() ��
��
��60����ʱ����ˮ���ڵ��¶�ԼΪ40��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס������������IJ������װ��3����С��������ȫ��ͬ��С�����м״��е�С���Ϸֱ��������0��1��2���Ҵ��е�С���Ϸֱ�������֩�1����2��0���ִӼ״�����������һ��С������е�����Ϊx���ٴ��Ҵ�����������һ��С������е�����Ϊy���Դ�ȷ����M�����꣨x��y����
��1�������û���״ͼ���б��ķ�����д����M���п��ܵ����ꣻ
��2�����M��x��y���ں���y=�� ![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
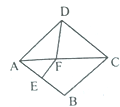
����Ŀ����ͼ��������ABCD�У���BAD=80![]() ��AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�F������Ϊ��E������DF�����CDF�Ķ�����____.
��AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�F������Ϊ��E������DF�����CDF�Ķ�����____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������й���һ���Ľ�ħ�������������40%���ۣ�Ϊ�����������������������о�������۳��ۣ���ʱÿ��ħ�����ۼ�Ϊ28Ԫ.
��1����ħ���Ľ��ۣ�
��2����������һ������ø���˫ʮһ�������̵������ʣ�µ�ħ����ÿ3��80Ԫ�ļ۸���ۣ��ܿ�����һ�գ�����ħ�����й�����2800Ԫ����ó��й�����ħ�����ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����̨�����ӹ���ͬ������������ӹ�160��������õ�ʱ�����һ����ӹ�120��������õ�ʱ����ȣ���֪�ס�����̨����ÿСʱ���ӹ�35���������ס�����̨����ÿСʱ���ӹ����ٸ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ű�����ȫ��ͬ��ֽ��A��B��C��D�У���������ֱ����ĸ���ͬ�ļ���ͼ�Σ���ͼ����С������4��ֽ�Ʊ��泯��ϴ�Ⱥ�����һ�ţ����Żأ����ٴ����µ�3��ֽ��������һ�ţ�
��1������״ͼ�����б�������ʾ�����������п��ܳ��ֵĽ����ֽ�ƿ���A��B��C��D��ʾ����
��2������������ֽ����������������ͼ�Σ�������Գ�ͼ���������ĶԳ�ͼ�εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCDEF�ı߳�Ϊ6cm��P�ǶԽ���BE��һ���㣬����P��ֱ��l��BE��ֱ������P��B���������1cm/s���ٶ�����ƽ����E�㣮��ֱ��lɨ����������ABCDEF��������ΪS��cm2������P���˶�ʱ��Ϊt��s���������ܷ�ӳS��t֮�亯����ϵ�Ĵ���ͼ���ǣ� ��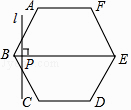
A.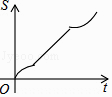
B.
C.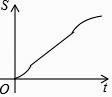
D.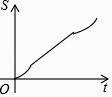
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2����a��1��x+a��2������a�dz����� 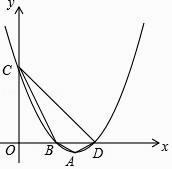
��1����֤������aΪ��ֵ���ö��κ�����ͼ����x��һ���й����㣻
��2����a=4ʱ���ö��κ�����ͼ��ΪA����x�ύ��B��D���㣬��y�ύ��C�㣬���ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ж�AB��CD�������У� ������
��1����B+��BCD=180������2����1=��2����3����3=��4����4����B=��5��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com