
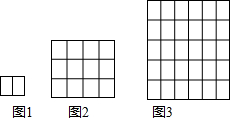
 这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用34块木块才能把第四次所铺的完全围起来.
这样铺地板:第一块铺2块,如图1,第二次把第一次的完全围起来,如图2;第三次把第二次的完全围起来,如图3;…依次方法,铺第5次时需用34块木块才能把第四次所铺的完全围起来. 分析 观察图形发现:若要将前一个图形包起来,上下各需要添一层,左右各需添一层,结合图1两块木块可以得出图n需要木块数为[1+(n-1)×2]×[2+(n-1)×2],求出图4图5所需木块数,二者相减即可得出结论.
解答 解:若要将前一个图形包起来,上下各需要添一层,左右各需添一层,
即图1木块个数为1×2,图2木块个数为(1+2)×(2+2),图3木块个数为(1+2×2)×(2+2×2),…,图n木块个数为[1+(n-1)×2]×[2+(n-1)×2].
由上面规律可知:图4需要木块个数为(1+3×2)×(2+3×2)=56(块),图5需要木块个数为(1+4×2)×(2+4×2)=90(块),
故铺第5次时需用90-56=34块木块才能把第四次所铺的完全围起来.
故答案为:34块.
点评 本题考查了图形的变化,解题的关键是:找出“图n需要木块数为[1+(n-1)×2]×[2+(n-1)×2]”这一规律.本题属于中档题,解决该类题型需要仔细观察图形,得出图形的变化规律,再结合规律找出结论.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
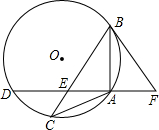 已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC中,内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
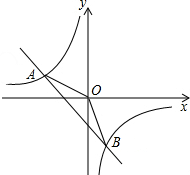 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$图象交于A(-2,1)、B(n,-2)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$图象交于A(-2,1)、B(n,-2)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 36×104 | B. | 3.6×104 | C. | 0.36×105 | D. | 3.6×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
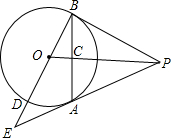 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,
如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点B,延长BO与⊙O交于点D,与PA的延长线交于点E,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com