
【题目】如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
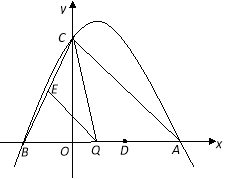
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ,当△CQE的面积为3时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)、y=-x2+x+4;(2)、Q(1,0);(3)、P(1+,2 )或P(1-,2 )或P(1+,3)或P(1-,3).
【解析】
试题分析:(1)、首先将A、C两点代入求出函数解析式;(2)、首先根据函数解析式得出点B的坐标,求出AB和BQ的长度,根据QE∥AC得出△BQE和△BAC相似得出EG的长度,然后根据三角形的面积得出点m的值,即得到点Q的坐标;(3)、根据DO=DF,FO=FD,OD=OF三种情况分别进行计算,得出点P的坐标.
试题解析:(1)由题意,得![]() ,解得
,解得![]() , ∴所求抛物线的解析式为y=-x2+x+4
, ∴所求抛物线的解析式为y=-x2+x+4
(2)如图,设点Q的坐标为(m,0),过点E作EG⊥x轴于点G,由-x2+x+4=0,
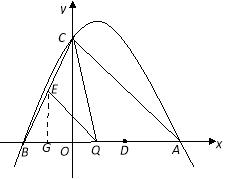
得x1=-2,x2=4,∴点B的坐标为(-2,0) ,∴AB=6,BQ= m +2
∵QE∥AC, ∴△BQE∽△BAC ,∴= 即=,∴EG=
∴ S△CQE=S△CBQ-S△EBQ=BQ·CO-BQ·EG =(m+2)(4-) =-m2+m+=3,
∴ m2-2m-8=-9, ∴m=1 ∴Q(1,0)
(3)存在
在△ODF中,
①若DO=DF,∵A(4,0),D(2,0),∴AD=OD=DF=2,又在Rt△AOC中,OA=OC=4,∴∠OAC= 45°
∴∠DFA=∠OAC= 45°∴∠ADF=90°此时,点F的坐标为(2,2)
由![]() ,得x1=1+,x2=1-
,得x1=1+,x2=1-
此时,点P的坐标为:P(1+,2 )或P(1-,2 )
②如图,
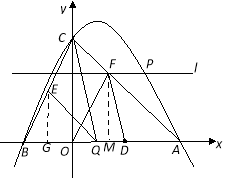
若FO=FD,过点F作FM⊥ 轴于点M,由等腰三角形的性质得:OM=OD=1,∴AM=3
∴在等腰直角三角形△AMF中,MF=AM=3 ∴F(1,3)
由-x2+x+4=3,得x1=1+,x2=1-
此时,点P的坐标为:P(1+,3)或P(1-,3)
③若OD=OF,∵OA=OC=4,且∠AOC=90°,∴AC= 4
∴点O到AC的距离为2,而OF=OD=2<2
此时,不存在这样的直线l,使得△ODF是等腰三角形.
综上所述,存在这样的直线l,使得△ODF是等腰三角形.所求点P的坐标为:
P(1+,2 )或P(1-,2 )或P(1+,3)或P(1-,3)


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】一棵树高h(m)与生长时间n(年)之间满足一定的关系,请你根据下表中的数写出 h(m)与n(年)之间的关系式:h=____.
n(年) | 2 | 4 | 6 | 8 | 10 | … |
h(m) | 2.6 | 3.2 | 3.8 | 4.4 | 5.0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如表:这些运动员跳高成绩的中位数和众数分别是( )
跳高成绩(m) | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 | 1.75 |
跳高人数 | 1 | 3 | 2 | 3 | 5 | 1 |
A. 1.65,1.70 B. 1.70,1.65 C. 1.70,1.70 D. 3,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次课堂练习,王莉同学做了如下4道分解因式题,你认为王莉做得不够完整的一题是( )
A. x3-x=x(x2-1) B. x2-2xy+y2=(x-y)2
C. x2y-xy2=xy(x-y) D. x2-y2=(x-y)(x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知小华上学期语文、数学、英语三科平均分为92分,他记得语文得了88分,英语得了95分,但他把数学成绩忘记了,你能告诉他应该是以下哪个分数吗?( )
A.93
B.95
C.94
D.96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com