
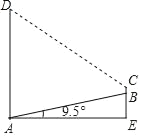
【题目】如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.(参考数据:sin19.5°≈![]() ,tan19.5°≈
,tan19.5°≈![]() ,最终结果精确到0.1m).
,最终结果精确到0.1m).
科目:初中数学 来源: 题型:
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
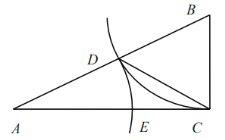
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
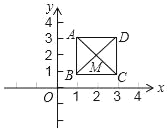
【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移一个单位”为一次变换.如此这样,连续经过2018次变换后,正方形ABCD的对角线交点M的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,该抛物线的顶点
,该抛物线的顶点![]() 的纵坐标是
的纵坐标是![]() .
.

(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)设直线与直线![]() 关于该抛物线的对称轴对称,求直线的表达式;
关于该抛物线的对称轴对称,求直线的表达式;
(3)平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 、
、![]() ,与直线交于点
,与直线交于点![]() .若
.若![]() ,结合函数图象,求
,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
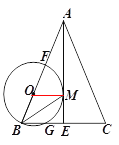
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com