
【题目】如图,正五边形的边长为2,连接对角线AD,BE,CE.线段AD分别与BE,CE相交于点M,N.给出下列结论:①△ABM≌△DCN;②DM2=DNAD;③MN=3+![]() ;④四边形ANCB为菱形.其中正确的是_____
;④四边形ANCB为菱形.其中正确的是_____

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(2011?菏泽)如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
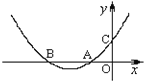
A. a+b=﹣1 B. a﹣b=﹣1
C. b<2a D. ac<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
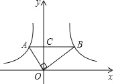
【题目】如图,在函数y1=![]() (x<0)和y2=
(x<0)和y2=![]() (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=![]() ,S△BOC=
,S△BOC=![]() ,则线段AB的长度=__.
,则线段AB的长度=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的“杨辉三角”告诉了我们二项式乘方展开式的系数规律,如:第三行的三个数(1、2、1)恰好对应着(a+b)2的展开式a2+2ab+b2的系数;第四行的四个数恰好对应着(a+b)3=a3+3a2b+3ab2+b3的系数,根据数表中前五行的数字所反映的规律,回答:
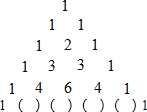
(1)图中第六行括号里的数字分别是 ;(请按从左到右的顺序填写)
(2)(a+b)4= ;
(3)利用上面的规律计算求值:(![]() )4﹣4×(
)4﹣4×(![]() )3+6×(
)3+6×(![]() )2﹣4×
)2﹣4×![]() +1.
+1.
(4)若(2x﹣1)2018=a1x2018+a2x2017+a3x2016+……+a2017x2+a2018x+a2019,求a1+a2+a3+……+a2017+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
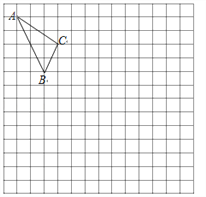
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
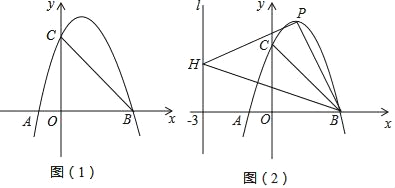
【题目】如图(1),已知抛物线E:y=ax2+bx+c与x轴交于A,B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),对称轴为直线x=1.
(1)填空:a= ,b= ,c= ;
(2)将抛物线E向下平移d个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求d的取值范围;
(3)如图(2),设点P是抛物线E上任意一点,点H在直线x=﹣3上,△PBH能否成为以点P为直角顶点的等腰直角三角形?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
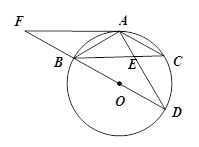
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家今年种植的“夏黑”葡萄喜获丰收,采摘上市后若干天便全部销完.小明对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(千克)与上市时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少15千克.
(1)第16天的日销售量是 千克.
(2)求y与x之间的函数关系式,并写出x的取值范围;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com