
【题目】已知,在矩形ABCD中,AB=a,BC=b,动点M从点A出发沿边AD向点D运动(点M与点A、点D不重合).
(1)如图1,当b=2a,点M运动到边AD的中点时,请证明∠BMC=90°;
(2)如图2,当a=2,b=5,求点M运动到什么位置时,∠BMC=90°;
(3)如图3,在第(2)问的条件下,若另一动点N从点C出发沿边C→M→B运动,且点M、点N的出发时间与运动速度都相同,过点N作AD和垂线交AD于点H,当△MNH与△MBC相似时,求MH的长.
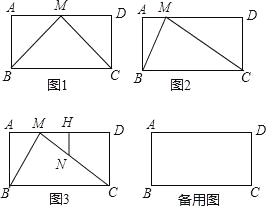
【答案】(1)详见解析;(2)AM=1或4时,∠BMC=90°;(3)△MNH与△MBC相似时,MH=8﹣![]() 或
或![]() ﹣2.
﹣2.
【解析】
试题分析:(1)由b=2a,点M是AD的中点,可得AB=AM=MD=DC=a,又由四边形ABCD是矩形,即可求得∠AMB=∠DMC=45°,则可求得∠BMC=90°;(2)根据已知条件得到∠AMB+∠DMC=90°,根据余角的性质得到∠ABM=∠DMC,根据相似三角形的性质得到![]() ,代入数据即可得到结论.(3)①当点N在CM上时,由△MNH与△MBC相似,得到∠BMC=∠MHN=90°,当AM=CN=1时,根据相似三角形的性质列方程求得结论;当AM=CN=4时,DM=1,CM=
,代入数据即可得到结论.(3)①当点N在CM上时,由△MNH与△MBC相似,得到∠BMC=∠MHN=90°,当AM=CN=1时,根据相似三角形的性质列方程求得结论;当AM=CN=4时,DM=1,CM=![]() <4,这种情况不存在;②当点N在BM上时,当AM=CN=1时,同理这种情况不存在;当AM=CN=4时,即CM+MN=4,根据相似三角形的性质即可得到结论.
<4,这种情况不存在;②当点N在BM上时,当AM=CN=1时,同理这种情况不存在;当AM=CN=4时,即CM+MN=4,根据相似三角形的性质即可得到结论.
试题解析:(1)证明:∵b=2a,点M是AD的中点,
∴AB=AM=MD=DC=a,
又∵在矩形ABCD中,∠A=∠D=90°,
∴∠AMB=∠DMC=45°,
∴∠BMC=90°.
(2)解:若∠BMC=90°,
则∠AMB+∠DMC=90°,
又∵∠AMB+∠ABM=90°,
∴∠ABM=∠DMC,
又∵∠A=∠D=90°,
∴△ABM∽△DMC,
∴![]() ,
,
设AM=x,则![]() ,
,
∴x=1或4,
∴AM=1或4时,∠BMC=90°;
(3)解:①当点N在CM上时,
∵△MNH与△MBC相似,
∴∠BMC=∠MHN=90°,
当AM=CN=1时,
∴DM=4,∴CM=2![]() ,
,
∴MN=2![]() ﹣1,
﹣1,
∵NH⊥AD,∠D=90°,
∴NH∥CD,
∴![]() ,
,
∴![]() ,
,
∴MH=8﹣![]() ;
;
当AM=CN=4时,
DM=1,CM=![]() <4,
<4,
∴这种情况不存在;
②当点N在BM上时,
当AM=CN=1时,同理这种情况不存在;
当AM=CN=4时,即CM+MN=4,
∵CM=![]() ,
,
∴MN=4﹣![]() ,BM=2
,BM=2![]() ,
,
∵HN∥AB,
∴△MHN∽ABM,
∴![]() ,即
,即![]() ,
,
∴MH=![]() ﹣2.
﹣2.
综上所述:△MNH与△MBC相似时,MH=8﹣![]() 或
或![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
【题目】已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1
B.a=﹣5,b=1
C.a=5,b=﹣1
D.a=﹣5,b=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市去年有4.7万名考生参加了中考,为了解这些考生的数学成绩,从中抽取了4000名考生的数学成绩进行统计分析,以下说法正确的是( )
A. 这4000名考生是总体的一个样本
B. 这4.7万名考生的数学成绩是总体
C. 每位考生是个体
D. 抽取的4000名考生是样本容量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为治理大气污染,保护人民健康.某市积极行动,调整产业结构,压减钢铁生产总量,2013年某市钢铁生产量为9700万吨,计划到2015年钢铁生产量设定为5000万吨,设该市每年钢铁生产量平均降低率为x,依题意,下面所列方程正确的是( )
A.9700(1﹣2x)=5000
B.5000(1+x)2=9700
C.5000(1﹣2x)=9700
D.9700(1﹣x)2=5000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在6×6的方格纸中,给出如下三种变换:P变换,Q变换,R变换.将图形F沿x轴向右平移1格得到图形F1,称为作1次P变换;将图形F沿y轴翻折得到图形F2,称为作1次Q变换;将图形F绕坐标原点顺时针旋转90°得到图形F3,称为作1次R变换.规定:PQ变换表示先作1次Q变换,再作1次P变换;QP变换表示先作1次P变换,再作1次Q变换;Rn变换表示作n次R变换,解答下列问题:
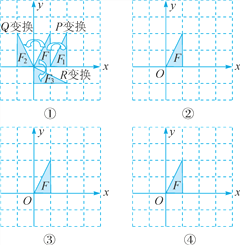
(1)作R4变换相当于至少作__ __次Q变换.
(2)请在图②中画出图形F作R2017变换后得到的图形F4.
(3)PQ变换与QP变换是否是相同的变换?请在图③中画出PQ变换后得到的图形F5,在图④中画出QP变换后得到的图形F6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com