
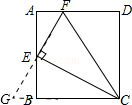
 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:| BC |
| CD |
| ||
| 2 |
|
| BC |
| CD |
| ||
| 2 |
|


科目:初中数学 来源: 题型:
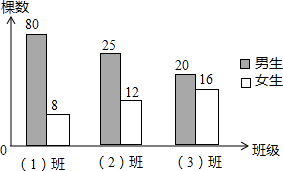 为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是
为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是查看答案和解析>>
科目:初中数学 来源: 题型:
 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20(
一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
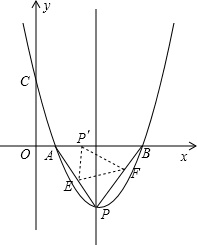 已知:抛物线经过A(2,0)、B(8,0)、C(0,
已知:抛物线经过A(2,0)、B(8,0)、C(0,16
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com