

分析 (1)根据∠POB=∠MOP-∠AOB代入数据即可求出结论;
(2)根据∠PON=180°-∠MOP可算出∠PON的度数,根据OB平分∠PON即可求出∠POB的度数,再通过角的计算可得出∠AOP=60°,结合∠MOP=120°即可得出∠AOP=$\frac{1}{2}$∠MOP,从而得出OA平分∠MOP;
(3)设∠AON=x°,则∠BON=90°-x°,∠POA=60°-x°,二者做差即可得出结论.
解答 解:(1)∠POB=∠MOP-∠AOB=120°-90°=30°.
故答案为:30°.
(2)OA平分∠MOP,理由如下:
∵∠MOP=120°,
∴∠PON=180°-∠MOP=60°.
∵OB平分∠PON,
∴∠POB=$\frac{1}{2}$∠PON=30°,∠AOP=∠AOB-∠POB=60°,
∵∠MOP=120°,
∴∠AOP=$\frac{1}{2}$∠MOP,
∴OA平分∠MOP.
(3)设∠AON=x°,则∠BON=90°-x°,∠POA=60°-x°,
∴∠BON-∠POA=(90°-x°)-(60°-x°)=30°.
点评 本题考查了余角和补角以及角的计算,通过角的计算找出各角之间的关系是解题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
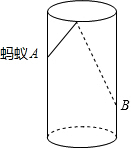 如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?
如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.
某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com