
【题目】如图,正方形ABCD中,M为BC上的点,E是AD的延长线的点,且AE=AM,过E作EF⊥AM垂足为F,EF交DC于点N.

(1)求证:AF=BM;
(2)若AB=12,AF=5,求DE的长.
【答案】(1)见解析;(2)DE=1.
【解析】
(1)由正方形的性质和已知可得∠ABC=∠AFE=90°,由AD∥BC得∠AMB=∠EAF,根据“AAS”可证△ABM≌△EFA,可得AF=BM;
(2)由勾股定理可求AM=13,由全等三角形的性质可得AM=AE=13,即可求DE的长.
(1)证明:∵四边形ABCD是正方形
∴∠ABC=90°,AD∥BC
∴∠EAF=∠AMB,
∵EF⊥AM,
∴∠AFE=∠ABC=90°,
在△ABM和△EFA中,
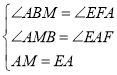 ,
,
∴△ABM≌△EFA(AAS)
∴AF=BM;
(2)解:∵AF=5,
∴BM=AF =5,
在Rt△ABM中,AB=12, BM=5,
∴AM=![]() ,
,
∴AE =AM= 13,
∵四边形ABCD是正方形,
∴AD =AB=12,
∴DE=AEAD=1312=1.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:对于一个关于![]() 的一元二次方程
的一元二次方程![]() (其中a≠0,a、b、c为常数)的两根分别为
(其中a≠0,a、b、c为常数)的两根分别为![]() ,
,![]() ,我们有如下发现①若
,我们有如下发现①若![]() ,
,![]() 为整数,则这个一元二次方程的判别式
为整数,则这个一元二次方程的判别式![]() 一定为完全平方数;②
一定为完全平方数;② ![]() ,
,![]() 满足韦达定理:即
满足韦达定理:即![]() ,
,![]() ;
;
③韦达定理也有逆定理,即如果两数![]() 和
和![]() 满足如下关系:
满足如下关系:![]() ,
,![]() ,那么这两个数
,那么这两个数![]() 和
和![]() 是方程
是方程![]() (
(![]() )的两个根.
)的两个根.
请应用上述材料解决以下问题:
(1)若实数![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,
的两个根,
①当![]() 时,则
时,则![]() ,
,![]() ;
;
②若![]() 均为整数且
均为整数且![]() ,求
,求![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
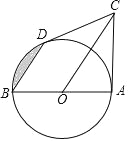
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
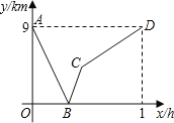
【题目】小明骑电动车从甲地去乙地,而小刚骑自行车从乙地去甲地,两人同时出发走相同的路线;设小刚行驶的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系,点B的坐标为(![]() ,0).根据图象进行探究:
,0).根据图象进行探究:
(1)两地之间的距离为______km;
(2)请解释图中点B的实际意义;
(3)求两人的速度分别是每小时多少km?
(4)直接写出点C的坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①b2>4ac;②4a+b=0;③函数图象与x轴的另一个交点为(2,0);④若点(﹣4,y1)、(﹣1,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是( )
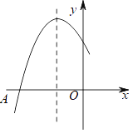
A. ②④ B. ①④ C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
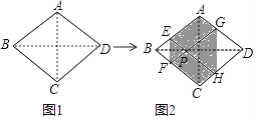
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;②当x= ![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com