
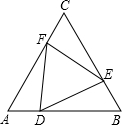
 如图,已知△ABC是等边三角形,边长为10,点D、E、F分别在边AB、BC、AC上,且AD=BE=CF,
如图,已知△ABC是等边三角形,边长为10,点D、E、F分别在边AB、BC、AC上,且AD=BE=CF,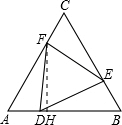 解:(1)∵AD为x,AD=BE=CF,
解:(1)∵AD为x,AD=BE=CF, ,
,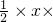 (10-x)×
(10-x)× =-
=- +
+ x,
x, =
=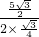 =5,
=5, =
=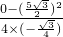 =
=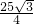 ,
,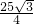 ;
;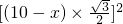 +x2=(10-x)2,
+x2=(10-x)2, ;
;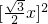 +(10-x)2=x2,
+(10-x)2=x2, ;
; 或
或 时,△ADF是直角三角形.
时,△ADF是直角三角形. ,△ADF的面积为y=-
,△ADF的面积为y=- +5x,根据二次函数的最值公式,即可求出当x为何值时,△ADF的面积最大值;
+5x,根据二次函数的最值公式,即可求出当x为何值时,△ADF的面积最大值;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 的坐标为(-1,0).
的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:
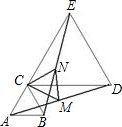 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com