
分析 分为2x+3=1,2x+3=-1,x+2016=0三种情况求解即可.
解答 解:①当2x+3=1时,解得:x=-1,此时x+2016=2015,则(2x+3)x+2016=12015=1,所以x=-1.
②当2x+3=-1时,解得:x=-2,此时x+2016=2014,则(2x+3)x+2016=(-1)2014=1,所以x=-2.
③当x+2016=0时,x=-2016,此时2x+3=-4029,则(2x+3)x+2016=(-4029)0=1,所以x=-2016.
综上所述,当x=-1,或x=-2,或x=-2016时,代数式(2x+3)x+2016的值为1.
点评 本题主要考查的是零指数幂的性质、有理数的乘方,分类讨论是解题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.
如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AD、AE分别是△ABC的中线和角平分线,AC=2,AB=5,过点C作CF⊥AE于点F,连接DF,有下列结论:
如图,AD、AE分别是△ABC的中线和角平分线,AC=2,AB=5,过点C作CF⊥AE于点F,连接DF,有下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
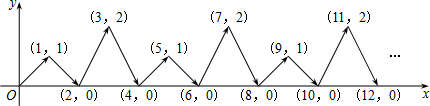
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
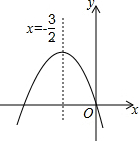 如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.
如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
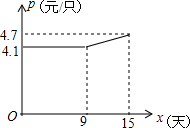 某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.
某企业接到一批茶杯生产任务,按要求在15天内完成,预定这批茶杯的出厂价为每个6元,为按时完成任务,该企业招收了新工人,设新工人小王第x天生产的茶杯数量为y个,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com