
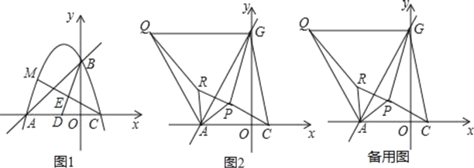
°æƒø°ø“—÷™≈◊ŒÔœfly=©Åx2©Å2x+3Ωªx÷·”⁄µ„A°¢C£®µ„A‘⁄µ„C◊Û≤‡£©£¨Ωªy÷·”⁄µ„B£Æ
£®1£©«ÛA£¨B£¨C»˝µ„◊¯±Í£ª
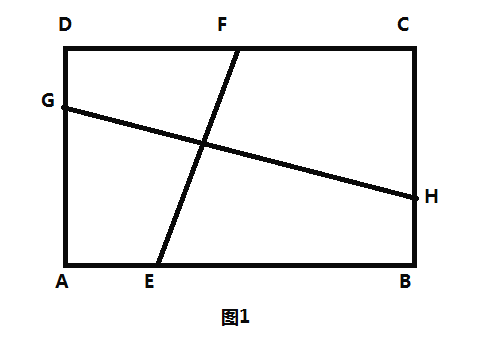
£®2£©»ÁÕº1£¨µ„DŒ™AC÷–µ„£¨µ„E‘⁄œfl∂ŒBD…œ£¨«“BE=2DE£¨¡¨Ω”CE≤¢—”≥§Ωª≈◊ŒÔœfl”⁄µ„M£¨«Ûµ„M◊¯±Í£ª
£®3£©»ÁÕº2£¨Ω´÷±œflAB»∆µ„A∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™15°„∫ÛΩªy÷·”⁄µ„G£¨¡¨Ω”CG£¨µ„PŒ™°˜ACGƒ⁄“ªµ„£¨¡¨Ω”PA°¢PC°¢PG£¨∑÷±“‘AP°¢AGŒ™±fl£¨‘⁄À¸√«µƒ◊Û≤‡◊˜µ»±fl°˜APR∫Õµ»±fl°˜AGQ£¨«ÛPA+PC+PGµƒ◊Ó–°÷µ£¨≤¢«Ûµ±PA+PC+PG»°µ√◊Ó–°÷µ ±µ„Pµƒ◊¯±Í£®÷±Ω”–¥≥ˆΩ·π˚º¥ø…£©£Æ
°æ¥∞∏°ø£®1£©A£®©Å3£¨0£©£¨C£®1£¨0£©£¨B£®0£¨3£©£ª£®2£©M£®©Å![]() £¨
£¨![]() £©£ª£®3£©2
£©£ª£®3£©2![]() ,P£®©Å
,P£®©Å![]() £¨
£¨![]() £©£Æ
£©£Æ
°æΩ‚Œˆ°ø
£®1£©≈◊ŒÔœfl![]() ÷–£¨¡Ó
÷–£¨¡Ó![]() £¨ø…µ√A£¨C◊¯±Í£ªµ±x=0 ±£¨ø…µ√Bµƒ◊¯±Í£ª
£¨ø…µ√A£¨C◊¯±Í£ªµ±x=0 ±£¨ø…µ√Bµƒ◊¯±Í£ª
£®2£© ◊œ»¿˚”√A°¢C◊¯±Í£¨«Û≥ˆDµƒ◊¯±Í£¨∏˘æ›BE=2ED£¨«Û≥ˆµ„E◊¯±Í£¨«Û≥ˆ÷±œflCE£¨¿˚”√∑Ω≥Ã◊È«ÛΩªµ„◊¯±ÍMº¥ø…£ª
£®3£©œ»÷§√˜°˜QAR°’°˜GAPº¥ø…µ√≥ˆQR=PG£¨Ω¯∂¯µ√µΩPA+PC+PG=PR+PC+QR£¨ø…µ√µ±Q£¨R£¨P£¨Cπ≤œfl ±£¨PA+PC+PGµƒ÷µ◊Ó–°£¨º¥Œ™œfl∂ŒQCµƒ≥§£¨◊˜QN°ÕOA”⁄N£¨AM°ÕQC”⁄M£¨PK°ÕOA”⁄K£¨¿˚”√π¥π…∂®¿Ì«Ûµ√QCµƒ≥§£¨‘Ÿ«Û≥ˆAM£¨CM£¨¿˚”√µ»±fl»˝Ω«–Œ–‘÷ «Û≥ˆAP°¢PM°¢PC£¨”…¥Àº¥ø…Ω‚æˆŒ £Æ
Ω‚£∫£®1£©≈◊ŒÔœfly=©Åx2©Å2x+3÷–£¨¡Óy=©Åx2©Å2x+3=0£¨ø…µ√x1=1£¨x2=©Å3£¨
°‡A£®©Å3£¨0£©£¨C£®1£¨0£©£¨
µ±x=0 ±£¨y=3£¨
°‡B£®0£¨3£©£ª
£®2£©°flµ„DŒ™AC÷–µ„£¨A£®©Å3£¨0£©£¨C£®1£¨0£©£¨
°‡D£®©Å1£¨0£©£¨
°flBE=2DE£¨B£®0£¨3£©£¨
°‡E£®©Å![]() £¨1£©£¨
£¨1£©£¨
…Ë÷±œflCEŒ™y=kx+b£¨∞—C£®1£¨0£©£¨E£®©Å![]() £¨1£©¥˙»Î£¨ø…µ√
£¨1£©¥˙»Î£¨ø…µ√
 £¨Ω‚µ√
£¨Ω‚µ√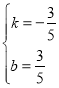 £¨
£¨
°‡÷±œflCEŒ™y=©Å![]() x+
x+![]() £¨
£¨
Ω‚∑Ω≥Ã◊È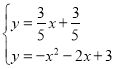 £¨ø…µ√
£¨ø…µ√![]() ªÚ
ªÚ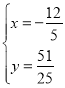 £¨
£¨
°flM‘⁄µ⁄∂˛œÛœfi£¨
°‡M£®©Å![]() £¨
£¨![]() £©£ª
£©£ª
£®3£©°fl°˜APR∫Õ°˜AGQ «µ»±fl»˝Ω«–Œ£¨
°‡AP=AR=PR£¨AQ=AG£¨°œQAG=°œRAP=60°„£¨
°‡°œQAR=°œGAP£¨
‘⁄°˜QAR∫Õ°˜GAP÷–£¨
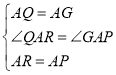 £¨
£¨
°‡°˜QAR°’°˜GAP£®SAS£©£¨
°‡QR=PG£¨
°‡PA+PC+PG=PR+PC+QR£¨
°‡µ±Q£¨R£¨P£¨Cπ≤œfl ±£¨PA+PC+PGµƒ÷µ◊Ó–°£¨º¥Œ™œfl∂ŒQCµƒ≥§£¨
»ÁÕº3£¨◊˜QN°ÕOA”⁄N£¨◊˜AM°ÕCQ”⁄M£¨◊˜PK°ÕCN”⁄K£¨
“¿Ã‚“‚µ√°œGAO=45°„+15°„=60°„£¨AO=3£¨
°‡AG=GQ=QA=6£¨°œAGO=30°„£¨OG=3![]() £¨
£¨
°fl°œAGQ=60°„£¨
°‡°œQGO=90°„£¨
°‡Q£®©Å6£¨3![]() £©£¨
£©£¨
‘⁄Rt°˜QNC÷–£¨QN=3![]() £¨CN=6+1=7£¨
£¨CN=6+1=7£¨
°‡QC=![]() =2
=2![]() £¨º¥PA+PC+PGµƒ◊Ó–°÷µŒ™2
£¨º¥PA+PC+PGµƒ◊Ó–°÷µŒ™2![]() £¨
£¨
°‡sin°œACM=![]() =
= ![]() £¨
£¨
°‡AM=![]() =
= ![]() £¨
£¨
°fl°˜APR «µ»±fl»˝Ω«–Œ£¨
°‡°œAPM=60°„£¨PM=![]() AM£¨MC=
AM£¨MC=![]() =
= ![]() £¨
£¨
°‡PC=CM©ÅPM=![]() £¨
£¨
°flsin°œPCN=![]() =
= ![]() £¨cos°œPCN=
£¨cos°œPCN=![]() =
= ![]() £¨
£¨
°‡PK=![]() £¨CK=
£¨CK=![]() £¨
£¨
°‡OK=![]() £¨
£¨
°‡P£®©Å![]() £¨
£¨![]() £©£Æ
£©£Æ


 »´ƒ‹≤‚øÿ∆⁄ƒ©–°◊¥‘™œµ¡–¥∞∏
»´ƒ‹≤‚øÿ∆⁄ƒ©–°◊¥‘™œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Ω´°˜ABC∑≈‘⁄√ø∏ˆ–°’˝∑Ω–Œµƒ±fl≥§Œ™1µƒÕ¯∏Ò÷–£¨µ„A£¨B£¨Cæ˘¬‰‘⁄∏Òµ„…œ£Æ
£®1£©°˜ABCµƒ√ʪ˝µ»”⁄____£ª
£®2£©«Î‘⁄»ÁÕºÀ˘ 浃կ∏Ò÷–£¨”√ŒfiøÃ∂»µƒ÷±≥fl£¨π˝µ„Aª≠“ªÃı÷±œfl£¨ΩªBC”⁄µ„D£¨ π°˜ABDµƒ√ʪ˝µ»”⁄°˜ADC√ʪ˝µƒ2±∂£¨≤¢ºÚ“™Àµ√˜ª≠Õºµƒ∑Ω∑®£®≤ª“™«Û÷§√˜£©£Æ___

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() «
«![]() µƒ÷±æ∂£¨«“
µƒ÷±æ∂£¨«“![]() £¨µ„
£¨µ„![]() Œ™
Œ™![]() Õ‚“ªµ„£¨«“
Õ‚“ªµ„£¨«“![]() £¨
£¨![]() ∑÷±«–
∑÷±«–![]() ”⁄µ„
”⁄µ„![]() °¢
°¢![]() ¡Ωµ„£Æ
¡Ωµ„£Æ![]() ”Î
”Î![]() µƒ—”≥§œflΩª”⁄µ„
µƒ—”≥§œflΩª”⁄µ„![]() £Æ
£Æ
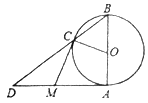
£®1£©«Û÷§£∫![]() £ª
£ª
£®2£©ÃÓø’
¢Ÿµ±![]() ________ ±£¨Àƒ±fl–Œ
________ ±£¨Àƒ±fl–Œ![]() «’˝∑Ω–Œ£Æ
«’˝∑Ω–Œ£Æ
¢⁄µ±![]() _________ ±£¨
_________ ±£¨![]() Œ™µ»±fl»˝Ω«–Œ£Æ
Œ™µ»±fl»˝Ω«–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®Œ «Èæ≥£©
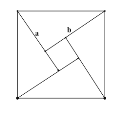
Œ“√«÷™µ¿»Ù“ª∏ˆæÿ–Œ «µƒ÷‹≥§πÃ∂®£¨µ±œ‡¡⁄¡Ω±flœ‡µ»£¨º¥Œ™’˝∑Ω–Œ ±£¨À¸µƒ√ʪ˝◊Ó¥Û£Æ∑¥π˝¿¥£¨»Ù“ª∏ˆæÿ–Œµƒ√ʪ˝πÃ∂®£¨À¸µƒ÷‹≥§ «∑Òª·”–◊Ó÷µƒÿ£ø
£®ÃΩæø∑Ω∑®£©
”√¡Ω∏ˆ÷±Ω«±fl∑÷±Œ™![]() £¨
£¨![]() µƒ4∏ˆ»´µ»µƒ÷±Ω«»˝Ω«–Œø…“‘∆¥≥…“ª∏ˆ’˝∑Ω–Œ°£»Ù
µƒ4∏ˆ»´µ»µƒ÷±Ω«»˝Ω«–Œø…“‘∆¥≥…“ª∏ˆ’˝∑Ω–Œ°£»Ù![]() £¨ø…“‘∆¥≥…»ÁÕºÀ˘ 浃’˝∑Ω–Œ£¨¥”∂¯µ√µΩ
£¨ø…“‘∆¥≥…»ÁÕºÀ˘ 浃’˝∑Ω–Œ£¨¥”∂¯µ√µΩ![]() £¨º¥
£¨º¥![]() £ªµ±
£ªµ±![]() ±£¨÷–º‰–°’˝∑Ω–Œ ’ÀıŒ™1∏ˆµ„£¨¥À ±’˝∑Ω–Œµƒ√ʪ˝µ»”⁄4∏ˆ÷±Ω«»˝Ω«–Œ√ʪ˝µƒ∫Õ.º¥
±£¨÷–º‰–°’˝∑Ω–Œ ’ÀıŒ™1∏ˆµ„£¨¥À ±’˝∑Ω–Œµƒ√ʪ˝µ»”⁄4∏ˆ÷±Ω«»˝Ω«–Œ√ʪ˝µƒ∫Õ.º¥![]() £Æ”⁄ «Œ“√«ø…“‘µ√µΩΩ·¬€£∫
£Æ”⁄ «Œ“√«ø…“‘µ√µΩΩ·¬€£∫![]() £¨
£¨![]() Œ™’˝ ˝£¨◊‹”–
Œ™’˝ ˝£¨◊‹”–![]() £¨µ±«“Ωˆµ±
£¨µ±«“Ωˆµ±![]() ±£¨¥˙ ˝ Ω
±£¨¥˙ ˝ Ω![]() »°µ√◊Ó–°÷µ
»°µ√◊Ó–°÷µ![]() £Æ¡ÌÕ‚£¨Œ“√«“≤ø…“‘Õ®π˝¥˙ ˝ Ω‘ÀÀ„µ√µΩ¿‡À∆…œ√ʵƒΩ·¬€£∫
£Æ¡ÌÕ‚£¨Œ“√«“≤ø…“‘Õ®π˝¥˙ ˝ Ω‘ÀÀ„µ√µΩ¿‡À∆…œ√ʵƒΩ·¬€£∫
°fl![]() £¨°‡
£¨°‡![]() £¨
£¨![]()
°‡∂‘”⁄»Œ“‚ µ ˝![]() £¨
£¨![]() ◊‹”–
◊‹”–![]() £¨«“µ±
£¨«“µ±![]() ±£¨¥˙ ˝ Ω
±£¨¥˙ ˝ Ω![]() »°◊Ó–°÷µ
»°◊Ó–°÷µ![]() £Æ
£Æ
πµ√…œ√ʵƒ∑Ω∑®£¨∂‘”⁄’˝ ˝![]() £¨
£¨![]() £¨ ‘±»Ωœ
£¨ ‘±»Ωœ![]() ∫Õ
∫Õ![]() µƒ¥Û–°πÿœµ£Æ
µƒ¥Û–°πÿœµ£Æ
£®¿‡±»”¶”√£©
¿˚”√…œ√ÊÀ˘µ√µΩµƒΩ·¬€ÕÍ≥…ÃÓø’
£®1£©µ±![]() ±£¨¥˙ ˝ Ω
±£¨¥˙ ˝ Ω![]() ”–◊Ó ÷µŒ™ £Æ
”–◊Ó ÷µŒ™ £Æ
£®2£©µ±![]() ±£¨¥˙ ˝ Ω
±£¨¥˙ ˝ Ω![]() ”–◊Ó ÷µŒ™ £Æ
”–◊Ó ÷µŒ™ £Æ
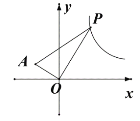
£®3£©»ÁÕº£¨“—÷™![]() «∑¥±»¿˝∫Ø ˝
«∑¥±»¿˝∫Ø ˝![]() ÕºœÛ…œ»Œ“‚“ª∂ص„£¨
ÕºœÛ…œ»Œ“‚“ª∂ص„£¨![]() £¨
£¨![]() £¨ ‘«Û
£¨ ‘«Û![]() µƒ◊Ó–°√ʪ˝£Æ
µƒ◊Ó–°√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
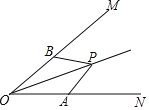
°æƒø°ø»ÁÕº£¨µ„P‘⁄°œMONµƒ∆Ω∑÷œfl…œ£¨µ„A°¢B‘⁄°œMONµƒ¡Ω±fl…œ£¨»Ù“™ π°˜AOP°’°˜BOP£¨ƒ«√¥–Ë“™Ã̺”“ª∏ˆÃıº˛ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
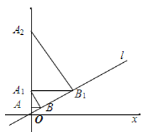
°æƒø°ø»ÁÕº£¨“—÷™÷±œfll£∫y=![]() x£¨π˝µ„A(0£¨1)◊˜y÷·µƒ¥πœflΩª÷±œfll”⁄µ„B£¨π˝µ„B◊˜÷±œfllµƒ¥πœflΩªy÷·”⁄µ„A1£ªπ˝µ„A1◊˜y÷·µƒ¥πœflΩª÷±œfll”⁄µ„B1£¨π˝µ„B1◊˜÷±œfllµƒ¥πœflΩªy÷·”⁄µ„A2£ª°≠°≠∞¥¥À◊˜∑®ºÃ–¯œ¬»•£¨‘Úµ„A2020µƒ◊¯±ÍŒ™______________£Æ
x£¨π˝µ„A(0£¨1)◊˜y÷·µƒ¥πœflΩª÷±œfll”⁄µ„B£¨π˝µ„B◊˜÷±œfllµƒ¥πœflΩªy÷·”⁄µ„A1£ªπ˝µ„A1◊˜y÷·µƒ¥πœflΩª÷±œfll”⁄µ„B1£¨π˝µ„B1◊˜÷±œfllµƒ¥πœflΩªy÷·”⁄µ„A2£ª°≠°≠∞¥¥À◊˜∑®ºÃ–¯œ¬»•£¨‘Úµ„A2020µƒ◊¯±ÍŒ™______________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
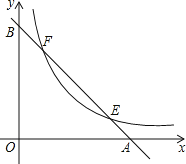
°æƒø°ø»ÁÕº£¨“—÷™÷±œfly£Ω©Åx+2∑÷±”Îx÷·£¨y÷·Ωª”⁄A£¨B¡Ωµ„£¨”ÎÀ´«˙œfly£Ω![]() Ωª”⁄E£¨F¡Ωµ„£¨»ÙAB£Ω2EF£¨‘Úkµƒ÷µ «_____£Æ
Ωª”⁄E£¨F¡Ωµ„£¨»ÙAB£Ω2EF£¨‘Úkµƒ÷µ «_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜ABC∂•µ„µƒ◊¯±Í∑÷±Œ™A£®©Å3£¨3£©£¨B£®©Å5£¨2£©£¨C£®©Å1£¨1£©£Æ
£®1£©“‘µ„CŒ™ŒªÀ∆÷––ƒ£¨◊˜≥ˆ°˜ABCµƒŒªÀ∆Õº–Œ°˜A1B1C£¨ π∆‰ŒªÀ∆±»Œ™1£∫2£¨«“ABCŒª”⁄µ„Cµƒ“Ï≤‡£¨≤¢±Ì æ≥ˆµ„A1µƒ◊¯±Í£Æ
£®2£©◊˜≥ˆ°˜ABC»∆µ„CÀ≥ ±’Ζ˝◊™90°„∫ÛµƒÕº–Œ°˜A2B2C£Æ
£®3£©‘⁄£®2£©µƒÃıº˛œ¬«Û≥ˆµ„Bæ≠π˝µƒ¬∑æ∂≥§£®Ω·π˚±£¡Ù¶–£©£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄æÿ–Œ![]() ÷–£¨
÷–£¨![]() µ„
µ„![]() ∑÷±‘⁄±fl
∑÷±‘⁄±fl![]() …œ£¨µ„
…œ£¨µ„![]() ∑÷±‘⁄±fl
∑÷±‘⁄±fl![]() …œ£¨«“
…œ£¨«“![]() £Æ
£Æ
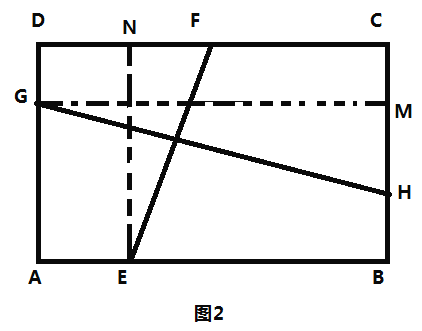
![]() »ÁÕº2£¨π˝µ„
»ÁÕº2£¨π˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() π˝µ„
π˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() ø…÷™Àƒ±fl–Œ
ø…÷™Àƒ±fl–Œ![]() Àƒ±fl–Œ
Àƒ±fl–Œ![]() Àƒ±fl–Œ
Àƒ±fl–Œ![]() Àƒ±fl–Œ
Àƒ±fl–Œ![]() ∂º «æÿ–Œ£¨º¥
∂º «æÿ–Œ£¨º¥![]()
![]() £¨Õ®π˝÷§√˜
£¨Õ®π˝÷§√˜![]() ø…«Ûµ√
ø…«Ûµ√![]() µƒ÷µŒ™_ £Æ
µƒ÷µŒ™_ £Æ
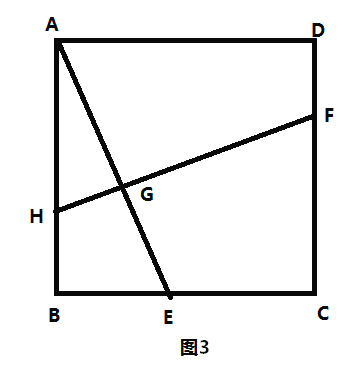
![]() »ÁÕº3£¨‘⁄’˝∑Ω–Œ
»ÁÕº3£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() ∑÷±‘⁄±fl
∑÷±‘⁄±fl![]() …œ£¨
…œ£¨![]() ”⁄µ„
”⁄µ„![]() £¨‘Ú
£¨‘Ú![]() µƒ÷µŒ™ £Æ
µƒ÷µŒ™ £Æ
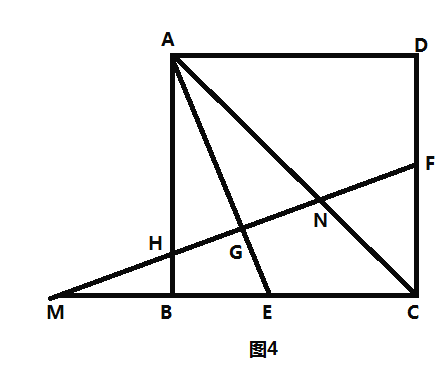
![]() »ÁÕº4£¨‘⁄
»ÁÕº4£¨‘⁄![]() µƒÃıº˛œ¬£¨—”≥§
µƒÃıº˛œ¬£¨—”≥§![]() Ωª
Ωª![]() µƒ—”≥§œfl”⁄µ„
µƒ—”≥§œfl”⁄µ„![]() ¡¨Ω”
¡¨Ω”![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £Æ»Ù
£Æ»Ù![]() «Û
«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com