
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 为
为![]() 外一点,且
外一点,且![]() ,
,![]() 分别切
分别切![]() 于点
于点![]() 、
、![]() 两点.
两点.![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
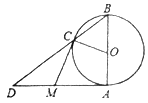
(1)求证:![]() ;
;
(2)填空
①当![]() ________时,四边形
________时,四边形![]() 是正方形.
是正方形.
②当![]() _________时,
_________时,![]() 为等边三角形.
为等边三角形.
【答案】(1)证明见解析;(2)6,![]() .
.
【解析】
(1)根据切线的性质及切线长定理可得MA⊥OA,MC⊥OC,MC=MA,然后根据等边对等角及等角的余角相等求出∠DCM=∠D,证得DM=MC即可得出结论;
(2)①根据正方形的判定定理可知当CM=OA=6时,四边形AOCM是正方形;
②根据等边三角形的性质可得∠D=60°,进而求出∠AOM=30°,然后解直角三角形求出AM即可解决问题.
解:(1)如图1,连接OM,
∵MA,MC分别切⊙O于点A、C,
∴MA⊥OA,MC⊥OC,MC=MA,
∴∠DCM+∠OCB=90°,∠D+∠B=90°,
∵OC=OB,
∴∠OCB=∠B,
∴∠DCM=∠D,
∴DM=MC,
∴DM=MA;
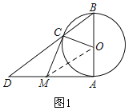
(2)①如图2,当CM=6时,四边形AOCM是正方形;
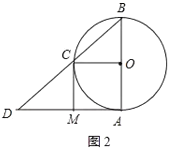
∵AB=12,
∴OA=OC=6,
又∵CM=AM=6,即AO=CO=AM=CM=6,
∴四边形AOCM是菱形,
又∵∠DAB=90°,
∴四边形AOCM是正方形;
②连接OM,如图3,
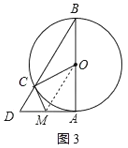
∵△DCM是等边三角形,
∴∠D=60°,
∵∠DAB=90°,
∴∠B=30°,
∴∠AOC=2∠B=60°,
∵AB=12,MA,MC分别切⊙O于点A、C,
∴OA=6,∠AOM=30°,
∴tan∠AOM=tan30°=![]() ,
,
∴AM=![]() ,
,
∴CM=AM=![]() ,
,
即当CM=![]() 时,△CDM为等边三角形.
时,△CDM为等边三角形.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图所示,下列说法中正确的是( )
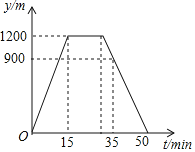
A. 小涛家离报亭的距离是900m
B. 小涛从家去报亭的平均速度是60m/min
C. 小涛从报亭返回家中的平均速度是80m/min
D. 小涛在报亭看报用了15min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(m﹣1)x﹣m,其中m>0,它的图象与x轴从左到右交于R和Q两点,与y轴交于点P,点O是坐标原点.下列判断中不正确的是( )
A.方程x2﹣(m﹣1)x﹣m=0一定有两个不相等的实数根B.点R的坐标一定是(﹣1,0)
C.△POQ是等腰直角三角形D.该二次函数图象的对称轴在直线x=﹣1的左側
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
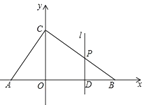
【题目】如图,在平面直角坐标系中,![]() 的斜边在
的斜边在![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上
轴上![]() ,
,![]() 、
、![]() 的长分别是一元二次方程
的长分别是一元二次方程![]() 的两个根,且
的两个根,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)在(2)的条件下,当![]() 时,请你直接写出点P的坐标.
时,请你直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县政府计划拨款34000元为福利院购买彩电和冰箱,已知商场彩电标价为2000元/台,冰箱标价为1800元/台,如按标价购买两种家电,恰好将拨款全部用完.
(1)问原计划购买的彩电和冰箱各多少台?
(2)购买的时候恰逢商场正在进行促销活动,全场家电均降价![]() 进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
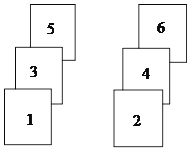
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2﹣2x+3交x轴于点A、C(点A在点C左侧),交y轴于点B.
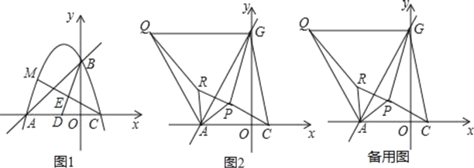
(1)求A,B,C三点坐标;
(2)如图1,点D为AC中点,点E在线段BD上,且BE=2DE,连接CE并延长交抛物线于点M,求点M坐标;
(3)如图2,将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,点P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在它们的左侧作等边△APR和等边△AGQ,求PA+PC+PG的最小值,并求当PA+PC+PG取得最小值时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为_____.
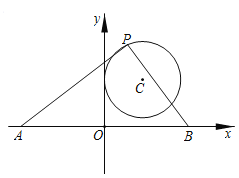
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com