
【题目】小亮步行上山游玩,设小亮出发x min加后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系,
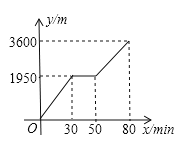
(1)小亮行走的总路程是____________m,他途中休息了____________min.
(2)当50![]() 80时,求y与x的函数关系式.
80时,求y与x的函数关系式.
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
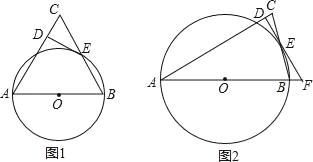
【题目】如图1,在△ABC中,AB=AC,以△ABC的边AB为直径的⊙O角边BC于点E,过点E作DE⊥AC交AC于D.
(1)求证:DE是⊙O的切线;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣![]() ,求⊙O的半径和EF的长.
,求⊙O的半径和EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点.
(1)已知点A(3,1),连接OA,作如下探究:
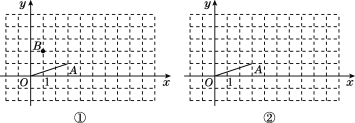
探究一:平移线段OA,使点O落在点B,设点A落在点C,若点B的坐标为(1,2),请在图①中作出BC,点C的坐标是__________.
探究二:将线段OA绕点O逆时针旋转90°,设点A落在点D,则点D的坐标是__________;连接AD,则AD=________(图②为备用图).
(2)已知四点O(0,0),A(a,b),C,B(c,d),顺次连接O,A,C,B,O,若所得到的四边形为平行四边形,则点C的坐标是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动支付快捷高效,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种,移动支付支付方式,为此在某步行街,使用某app,软件对使用移动支付的行人进行随机抽样调查,设置了四个选项,支付宝,微信,银行卡,其他移动支付(每人只选一项),以下是根据调查结果分别整理的不完整的条形统计图和扇形统计图.
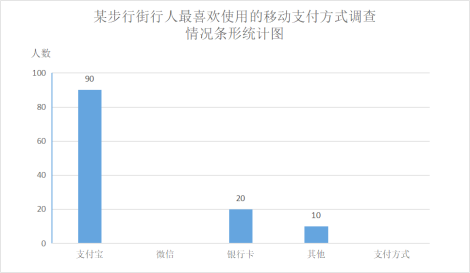

请你根据下列统计图提供的信息,完成下列问题.
(1)这次调查的样本容量是 ;
(2)请补全条形统计图;
(3)求在此次调查中表示使用微信支付的扇形所对的圆心角的度数.
(4)若某天该步行街人流量为10万人,其中40%的人购物并选择移动支付,请你依据此次调查获得的信息,估计一下当天使用银行卡支付的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
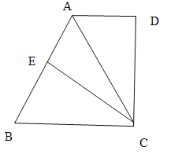
【题目】如图,在梯形ABCD中,∠BCD=∠D=90,上底AD=3,下底BC=![]() ,高CD=4,沿AC把梯形ABCD翻折,点D是恰好落在AB边上的点E处,求△BCE面积。
,高CD=4,沿AC把梯形ABCD翻折,点D是恰好落在AB边上的点E处,求△BCE面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小江家的住房户型结构图.根据结构图提供的信息,解答下列问题:
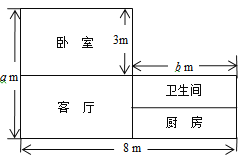
(1)用含a、b的代数式表示小江家的住房总面积S;
(2)小江家准备给房间重新铺设地砖.若卧室所用的地砖价格为每平方米50元;卫生间、厨房和客厅所用的地砖价格为每平方米40元.请用含a、b的代数式表示铺设地砖的总费用W;
(3)在(2)的条件下,当a=6,b=4时,求W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
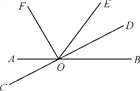
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.

(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 平均数是 中位数为
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com