
【题目】下面是“过圆外一点作圆的切线”的尺规作图过程.



请回答以下问题:
(1)连接OA,OB,可证∠OAP =∠OBP = 90°,理由是______________________;
(2)直线PA,PB是⊙O的切线,依据是__________________________________.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条笔直跑道上的A,B两处相距500米,甲从A处,乙从B处,两人同时相向匀速而跑,直到乙到达A处时停止,且甲的速度比乙大.甲、乙到A处的距离![]() (米)与跑动时间
(米)与跑动时间![]() (秒)的函数关系如图14所示.
(秒)的函数关系如图14所示.
(1)若点M的坐标(100,0),求乙从B处跑到A处的过程中![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若两人之间的距离不超过200米的时间持续了40秒.
①当![]() 时,两人相距200米,请在图14中画出P(
时,两人相距200米,请在图14中画出P(![]() ,0).保留画图痕迹,并写出画图步骤;
,0).保留画图痕迹,并写出画图步骤;
②请判断起跑后![]() 分钟,两人之间的距离能否超过420米,并说明理由.
分钟,两人之间的距离能否超过420米,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是人字型金属屋架的示意图,该屋架由BC、AC、BA、AD四段金属材料焊接而成,其中A、B、C、D四点均为焊接点,且AB=AC,D为BC的中点,假设焊接所需的四段金属材料已截好,并已标出BC段的中点D,那么,如果焊接工身边只有可检验直角的角尺,而又为了准确快速地焊接,他应该首先选取的两段金属材料及焊接点是( )
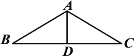
A.AB和AD,点AB.AB和AC,点B
C.AC和BC, 点CD.AD和BC,点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y = x2 - 4x + 3.
(1)用配方法将y = x2 - 4x + 3化成y = a(x - h)2 + k的形式;
(2)在平面直角坐标系![]() 中画出该函数的图象;
中画出该函数的图象;
(3)当0≤x≤3时,y的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()
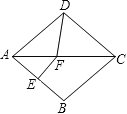
A.50°B.60°C.70°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2019按照一定规律排成下表:

记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a42= ,a53= ;
(2)①如果aij=2019,那么i= ,j= ;②用i,j表示aij= ;
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com