
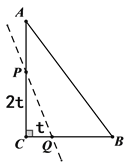
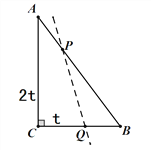
����Ŀ����ͼ����ABC�У���C=90�㣬AB=10cm��BC=6cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��2 cm/s�����˶���ʱ��Ϊt�룮
��1�������������BCP�ǵ���ֱ�������Σ���˵�����ɡ�
��2����t=_____________________ʱ����BCPΪ���������Σ�
��3������һ��Q���ӵ�C��ʼ����C��B��·���˶������ٶ�Ϊ1cm/s����P��Q����ͬʱ��������P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶�����tΪ��ֵʱ��ֱ��PQ����ABC���ܳ��ֳɵ�������֮����2����ϵ��



(����ͼ) (����ͼ)
���𰸡�(1)t=3,���ɼ���������2��3s, 5.4s, 6s��6.5s����3��t=![]() ��t=
��t=![]() .
.
�������������������1��������ó�BC=CP�����ɵó������
��2����BCPΪ����������ʱ������������������ۣ���CP=CB����BC=BP����PB=PC�����ɵó��𰸣�
��3����P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶����ó�0��t��6��C��ABC=24����ֱ��PQ�ѡ�ABC���ܳ��ֳɵ�������֮����1��2����һ����Ϊ8����һ����Ϊ16����������������ɵó��𰸣�
���������
(1) ����BCP�ǵ���ֱ��������
��BC=CP
��2t=6
t=3s
��2����t= 3s, 5.4s, 6s��6.5s ʱ����BCPΪ����������.
��3����P��Q����һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶���
��0��t��6
C��ABC=24
��ֱ��PQ�ѡ�ABC���ܳ��ֳɵ�������֮����1��2
��һ����Ϊ8����һ����Ϊ16
��t+2t=8, t=![]()
��t+2t=16, t=![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
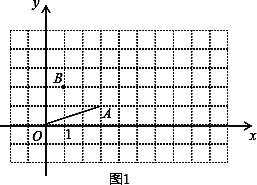
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣮
��1����֪��A(3��1)������OA��������̽����
̽��һ��ƽ���߶�OA��ʹ��O���ڵ�B.���A���ڵ�C,����B������Ϊ(1��2)������ͼ1������BC����C��������_________��
̽���������߶�OA�Ƶ�O��ʱ����ת90�㣬���A���ڵ�D.���D��������_______.
��2�� ��֪�ĵ�O(0��0)��A (a��b)�� C��B(c��d)��˳������O��A��C��B��
�����õ����ı����������Σ���ֱ��д��a��b��c��dӦ����Ĺ�ϵʽ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͳ�ƣ�2014���ҹ����¼�����Ʒ�����ܶ��40570��Ԫ��������40570���ÿ�ѧ��������ʾΪ��Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��x1��x2�Ƿ���x2+2x��3��0���������������ʽx12+3x1+x2��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�����ݵļ�������ʱ��Ӧ����㷺���ǣ�������
A.����
B.���
C.ƽ����
D.ȫ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ�
��abc��0
��4a+2b+c��0
��4ac��b2��8a
��![]() ��a��
��a��![]()
��b��c��
���к�������ȷ���۵�ѡ���ǣ� ��

A���٢� B���٢ۢ� C���ڢܢ� D���٢ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ж������������٣�������֤��
��1��������ǵĺ��Ƕ۽ǣ�
��2����a��b����a2��b2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com