
【题目】已知:一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的平均数是22,方差是13,那么另一组数据
的平均数是22,方差是13,那么另一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的方差是__________.
的方差是__________.
【答案】117.
【解析】
根据平均数,方差的公式进行计算.
解:依题意,得![]() =
=![]() =22,
=22,
∴![]() =110,
=110,
∴3a-2,3b-2,3c-2,3d-2,3e-2的平均数为
![]() =
=![]() =
=![]() ×(3×110-2×5)=64,
×(3×110-2×5)=64,
∵数据a,b,c,d,e的方差13,
S2=![]() [(a-22)2+(b-22)2+(c-22)2+(d-22)2+(e-22)2]=13,
[(a-22)2+(b-22)2+(c-22)2+(d-22)2+(e-22)2]=13,
∴数据3a-2,3b-2,3c-2,3d-2,3e-2方差
S′2=![]() [(3a-2-64)2+(3b-2-64)2+(3c-2-64)2+(3d-2-64)2+(3e-2-64)2]
[(3a-2-64)2+(3b-2-64)2+(3c-2-64)2+(3d-2-64)2+(3e-2-64)2]
=![]() [(a-22)2+(b-22)2+(c-22)2+(d-22)2+(e-22)2]×9
[(a-22)2+(b-22)2+(c-22)2+(d-22)2+(e-22)2]×9
=13×9
=117.
故答案为:117.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
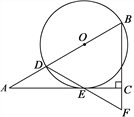
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
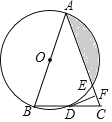
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,E在AD上,F在AB上,EF⊥CE于E,DE=AF=2,矩形的周长为24,则BF的长为( )
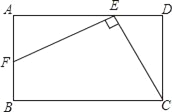
A. 3 B. 4 C. 5 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
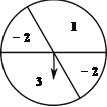
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.

(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
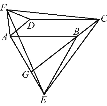
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0)中,函数 y 与自变量 x 的部分对应值如下表:
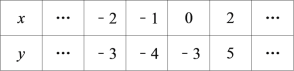
(1)求二次函数的解析式;
(2)求该函数图象与 x 轴的交点坐标;
(3)不等式 ax2+bx+c+3>0 的解集是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com