
(本题满分10分)如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.

(1)求证:∠ACM=∠ABC;
(2)延长BC到D,使BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的半径.
(1)详见解析;(2)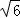
【解析】
试题分析:(1)如图,连接OC
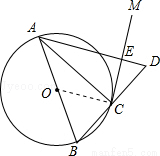
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ABC+∠BAC=90°,
又∵CM是⊙O的切线,
∴OC⊥CM,
∴∠ACM+∠ACO=90°,
∵CO=AO,
∴∠BAC=∠AOC,
∴∠ACM=∠ABC;
(2)∵BC=CD,∴OC∥AD,又∵OC⊥CE,
∴AD⊥CE,∴△AEC是直角三角形,∴△AEC的外接圆的直径是AC.
又∵∠ABC+∠BAC=90°,∠ACM+∠ECD=90°,
∴△ABC∽△CDE,∴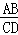 =
=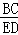 ,
,
⊙O的半径为3,∴AB=6,∴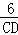 =
=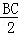 ,
,
∴BC2=12,∴BC=2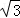 ,∴AC=
,∴AC=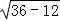 =2
=2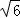 ,
,
∴△AEC的外接圆的半径为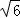 .
.
考点: 1.圆的性质;2.相似三角形的性质


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分6分)已知关于 的一元二次方程
的一元二次方程 (
( 为常数).
为常数).
(1)求证:方程有两个不相等的实数根;
(2)设 ,
, 为方程两个实数根,且
为方程两个实数根,且 ,试求出方程的两个实数根和
,试求出方程的两个实数根和 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分7分)已知代数式A=2x2+3xy+2y-1,B=x2-xy+x-
(1)当x=y=-2时,求A-2B的值;
(2)若A-2B的值与x的取值无关,求y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com