Question

如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM=CN，AM交BN于点P．

（1）求证：△ABM≌△BCN；

（2）求∠APN的度数．

 

 

Answer 1

（1）证明见解析；

（2）∠APN的度数为108°．

【解析】

试题分析：（1）利用正五边形的性质得出AB=BC，∠ABM=∠C，再利用全等三角形的判定得出即可；

（2）利用全等三角形的性质得出∠BAM+∠ABP=∠APN，进而得出∠CBN+∠ABP=∠APN=∠ABC即可得出答案．

试题解析：（1）∵正五边形ABCDE，

∴AB=BC，∠ABM=∠C，

∴在△ABM和△BCN中

，

∴△ABM≌△BCN（SAS）；

（2）∵△ABM≌△BCN，

∴∠BAM=∠CBN，

∵∠BAM+∠ABP=∠APN，

∴∠CBN+∠ABP=∠APN=∠ABC=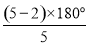=108°．

即∠APN的度数为108°．

考点：1.全等三角形的判定与性质2.多边形内角与外角．