
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:![]()
⑴根据如图1,写出一个等式:
⑵如图2,若长方形的长AB为10,AD宽为6,分别求a、b的值;
⑶如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=6,ab=10,请求出阴影部分的面积.



【答案】(1)![]() ;(2)a=2,b=4; (3)3.
;(2)a=2,b=4; (3)3.
【解析】
(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种是大矩形的面积,另一种可以是4个正方形的面积和5个矩形的面积,可得等式;
(2)根据长AB为10,宽AD为6列方程组求解即可;
(3)利用S阴影=正方形ABCD的面积+正方形ECGF的面积-三角形BGF的面积-三角形ABD的面积求解.
(1)(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5ab +2b2;
(2)∵长方形的长AB为10,宽AD为6,
∴![]() ,
,
解之得
![]() ;
;
(3)∵a+b=6,ab=10,
∴S阴影=a2+b2-![]() (a+b)b-
(a+b)b-![]() a2=
a2=![]() a2+
a2+![]() b2-
b2-![]() ab=
ab=![]() (a+b)2-
(a+b)2-![]() ab=
ab=![]() ×62-
×62-![]() ×10=18-15=3.
×10=18-15=3.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】[数学实验探索活动]
实验材料现有若干块如图①所示的正方形和长方形硬纸片.
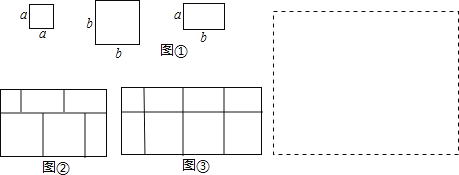
实验目的:
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,得到相应的等式,从而探求出多项式乘法或分解因式的新途径.
例如,选取正方形、长方形硬纸片共 6 块,拼出一个如图②的长方形,计算它的面积, 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2.
问题探索:
(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ,那么需要两种正方形纸片 张,长方形纸片 张;
(2)选取正方形、长方形硬纸片共 8 块,可以拼出一个如图③的长方形,计算图③的面积,并写出相应的等式;
(3)试借助拼图的方法,把二次三项式 2a2+5ab+2b2 分解因式,并把所拼的图形画在虚线方框内.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,四边形
为坐标原点,四边形![]() 是平行四边形,点
是平行四边形,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的动点,若
上的动点,若![]() 是等腰三角形,则点
是等腰三角形,则点![]() 的坐标为_____.
的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,对角线
在第一象限内,对角线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() .将菱形
.将菱形![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位.当点
个单位.当点![]() 落在
落在![]() 的内部时(不包括三角形的边),则
的内部时(不包括三角形的边),则![]() 的取值范围是__________.
的取值范围是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
⑴如图1,若AD∥BC,求证:BD∥AC;
⑵如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
⑶如图3,在⑵的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,正确的有( )
①经过三个点一定可以作圆;②任意一个三角形一定有一个外接圆,并且只有一个外接圆;③在同圆或等圆中,相等的弦则所对的弧相等;④正多边形既是中心对称图形又是轴对称图形;⑤三角形的内心到三角形各边的距离相等.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com