【题目】[数学实验探索活动]

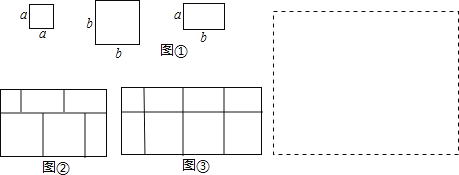
实验材料现有若干块如图①所示的正方形和长方形硬纸片．

实验目的：

用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径．

例如，选取正方形、长方形硬纸片共 6 块，拼出一个如图②的长方形，计算它的面积， 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2．

问题探索：

(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ，那么需要两种正方形纸片 张，长方形纸片 张；

(2)选取正方形、长方形硬纸片共 8 块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；

(3)试借助拼图的方法，把二次三项式 2a2+5ab+2b2 分解因式，并把所拼的图形画在虚线方框内.

参考答案：

【答案】（1）3,3；（2）a2+4ab+3b2=（a+3b）（a+b）；（3）2b2+5ab+2a2=（2b+a）（b+2a）．画图见解析.

【解析】

（1）根据多项式(2a+b)(a+b) =2a2+3ab+b2可发现矩形有两个小正方形，一个大正方形和三个小长方形.

（2）正方形、长方形硬纸片一共八块，面积等于长为a+3b，宽为a+b的矩形面积.所以a2+4ab+3b2=（a+3b）（a+b）

（3）正方形、长方形硬纸片共9块，画出图形，面积等于长为a+2b，宽为2a+b的矩形面积，则2a2+5ab+2b2=（2a+b）（a+2b）

（1）∵(2a+b)(a+b) =2a2+3ab+b2；

∴拼图需要两个小正方形，一个大正方形和三个小长方形

∴需要3个正方形纸片，3个长方形纸片.

（2）∵大长方形长为a+3b，宽为a+b

∴面积S=（a+3b）（a+b）

又∵大长方形由三个大正方形，一个小正方形和四个小长方形组成

∴面积S= a2+4ab+3b2

∴a2+4ab+3b2=（a+3b）（a+b）

（3）∵由2b2+5ab+2a2可知

大长方形由两个小正方形和两个大正方形以及五个长方形组成，如图

∴2b2+5ab+2a2=（2b+a）（b+2a）．

关闭