
����Ŀ����ͼ��ֱ��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
��2����PΪ�������ڵڶ�������һ�㣬����P��x��Ĵ��ߣ�����Ϊ��M����ֱ��AB���ڵ�C������P��x���ƽ���߽��������ڵ�Q������Q��x��Ĵ��ߣ�����Ϊ��N������P�ڵ�Q��ߣ����P�ĺ�����Ϊm��
�ٵ�����PQNM���ܳ����ʱ�����ACM�������
���ڢٵ������£�������PMNQ���ܳ����ʱ����ֱ��AC��һ��G��y���ƽ���߽�������һ��F���Ƿ���ڵ�F��ʹ���Ե�P��C��G��FΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1����ֱ��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��
��A����3��0����B��0��3����
��������y=��x2+bx+c����A��B���㣬
��![]() �����
�����![]() ��
��
�������ߵĽ���ʽΪy=��x2��2x+3��
��2���١ߵ�P�ĺ�����Ϊm��
��P��m����m2��2m+3����PM=��m2��2m+3��
��������y=��x2��2x+3�ĶԳ���Ϊx=��![]() =��
=��![]() =��1��
=��1��
��PQ=2����1��m��=��2m��2��
�����PQMN���ܳ�=2��PM+PQ��=2����m2��2m+3��2m��2��=��2m2��8m+2=��2��m+2��2+10��
��m=��2ʱ������PQMN���ܳ����ʱ��C������Ϊ����2��1����CM=AM=1��
��S��ACM=![]() ��1��1=
��1��1=![]() ��
��
�ڡ�C����2��1����
��P����2��3����
��PC=3��1=2��
�ߵ�P��C��G��FΪ������ı�����ƽ���ı��Σ�GF��y�ᣬ
��GF��PC����GF=PC��
��G��x��x+3������F��x����x2��2x+3����
����F�ڵ�G���Ϸ�ʱ����x2��2x+3����x+3��=2�����x=��1��x=��2����ȥ����
��x=��1ʱ����x2��2x+3=4����F1����1��4����
����F�ڵ�G���·�ʱ��x+3������x2��2x+3��=2�����x=![]() ��x=
��x=![]() ��
��
��x=![]() ʱ����x2��2x+3=
ʱ����x2��2x+3=![]() ��
��
��x=![]() ʱ����x2��2x+3=
ʱ����x2��2x+3=![]() ��
��
��F2��![]() ��
��![]() ����F3��
����F3��![]() ��
��![]() ����
����
������ʾ����F������ΪF1����1��4����F2��![]() ��
��![]() ����F3��
����F3��![]() ��
��![]() ����
����
����������1�������A��B��������꣬�ٴ���������y=��x2+bx+c���b��c��ֵ���ɣ�
��2��������m��ʾ��PM�ij�������������ߵĶԳ��ἰPQ�ij������þ��ε������ʽ�ɵó����ܳ��Ľ���ʽ�������ɵó�������������ֵ�����C�����꣬�������ε������ʽ���ɵó����ۣ�
�ڸ���C������ó�P�����꣬�ʿɵó�PC�ij����ٷֵ�F�ڵ�G���Ϸ����F�ڵ�G���·���������������ۼ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx+b��k��0�����㣨1��2��
��1����գ�b=�� �����ú�k����ʽ��ʾ����
��2������ֱ������ƽ��2����λ����ƽ�ƺ��ֱ�߽�x�ڵ�A����y�ڵ�B��x�������е�C��1+k��0����ʹ�á�ABC�����Ϊ2����kֵ��
��3����1��x��3������ֵy�ܴ����㣬��kȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[��ѧʵ��̽���]
ʵ������������ɿ���ͼ����ʾ�������κͳ�����ӲֽƬ��
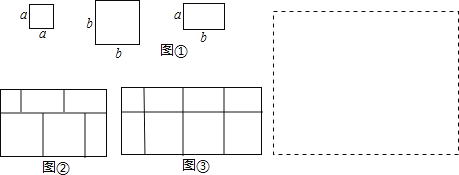
ʵ��Ŀ�ģ�
�����ɿ������������κͳ�����ӲֽƬƴ��һ���µij����Σ�ͨ����ͬ�ķ�������������õ���Ӧ�ĵ�ʽ���Ӷ�̽�������ʽ�˷���ֽ���ʽ����;����
���磬ѡȡ�����Ρ�������ӲֽƬ�� 6 �飬ƴ��һ����ͼ�ڵij����Σ�������������� д����Ӧ�ĵ�ʽ�� a2+3ab+2b2=(a+2b)(a+b)�� (a+2b)(a+b) =a2+3ab+2b2��
����̽����
(1) С������ƴͼ�ķ������Ͷ���ʽ�˷�(2a+b)(a+b) =2a2+3ab+b2 ����ô��Ҫ����������ֽƬ �ţ�������ֽƬ �ţ�
(2)ѡȡ�����Ρ�������ӲֽƬ�� 8 �飬����ƴ��һ����ͼ�۵ij����Σ�����ͼ�۵��������д����Ӧ�ĵ�ʽ��
(3)�Խ���ƴͼ�ķ������Ѷ�������ʽ 2a2+5ab+2b2 �ֽ���ʽ��������ƴ��ͼ�λ������߷�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�һ������1��2��4��8��16��32���������ִӵڶ��ʼ��ÿһ����ǰһ��ı�ֵ����ͬһ�����������������_______�����ݴ˹��ɣ����![]() (
(![]() Ϊ������)��ʾ������еĵ�
Ϊ������)��ʾ������еĵ�![]() ����
����![]() ��
��![]() ����ô
����ô![]() _____������
_____������![]() _______��
_______��
�������![]() ��ֵ��
��ֵ��
����![]() ����������
����������
����ʽ����ͬ����2����
![]() ������������
������������
�ɢڼ�ȥ��ʽ����![]() .
.
(2)��ȿɵã�![]() __________.
__________.
(3)�������һ��ķ���֪��������![]() ��
��![]() ��
��![]() ������
������![]() ���ӵڶ��ʼÿһ����ǰһ��֮�ȵij���Ϊ
���ӵڶ��ʼÿһ����ǰһ��֮�ȵij���Ϊ![]() ����ô
����ô![]() ��
��![]() ____������
____������![]() ______ (�ú�
______ (�ú�![]() ��
��![]() ��
��![]() �Ĵ���ʽ��ʾ).
�Ĵ���ʽ��ʾ).
�ú�![]() ��
��![]() ��
��![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() _________.
_________.
(4)һ�ʵ�Ӿ���ԭ��һ����λ��A����ԭ�㷽����������һ������OA�е�![]() �����ڶ��δ�
�����ڶ��δ�![]() ����
����![]() ���е�
���е�![]() ���������δ�
���������δ�![]() ����
����![]() ���е�
���е�![]() ����������˲�������ȥ�����50���������ʵ������ľ����Ƕ��٣�
����������˲�������ȥ�����50���������ʵ������ľ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�У�AB��AC��2����B��75������CΪ��ת���Ľ���ABC˳ʱ����ת������B����AB�ϵ�D��ʱ����A�Ķ�Ӧ��ΪE������Ӱ�������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��C����EF�ϣ�
��C����EF�ϣ�![]() ��BCƽ��
��BCƽ��![]() ����
����![]() �����н��ۣ�
�����н��ۣ�
��ACƽ��![]() ����
����![]() ����
����![]() ����
����![]() �����н�����ȷ�ĸ����У� ��
�����н�����ȷ�ĸ����У� ��

A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬�ı���
Ϊ����ԭ�㣬�ı���![]() ��ƽ���ı��Σ���
��ƽ���ı��Σ���![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() �ǵ��������Σ����
�ǵ��������Σ����![]() ������Ϊ_____��
������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪DC��FP����1����2����FED��28����AGF��80��FHƽ�֡�EFG��
(1)˵����DC��AB��
(2)���PFH�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����A�Ƿ���������y=-![]() ͼ����һ�㣬����A��x��Ĵ��ߣ�����ΪB�㣬��OA=2
ͼ����һ�㣬����A��x��Ĵ��ߣ�����ΪB�㣬��OA=2![]() ������AOB���ܳ�Ϊ________��
������AOB���ܳ�Ϊ________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com