
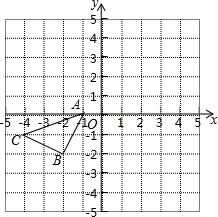
 如图,△ABC在平面直角坐标系中.
如图,△ABC在平面直角坐标系中.分析 (1)根据直角坐标系的特点写出各点的坐标;
(2)分别将点A、B、C向上平移2个单位,再向右平移2个单位得到点A′、B′、C′,然后顺次连接;
(3)用四边形的面积减去三个小三角形的面积即可求解.
解答 解:(1)A(-1,0),B(-2,-2),C(-4,-1);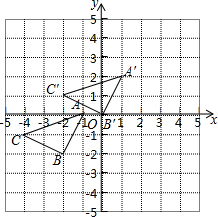
(2)所作图形如图所示:
A'(1,2),B'(0,0),C'(-2,1);
(3)S△ABC=2×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2
=$\frac{5}{2}$.
点评 本题考查了根据平移变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
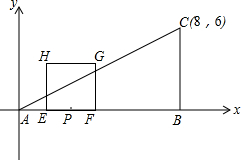 在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.
在Rt△ABC中,∠ABC=90°,以A为坐标原点,AB所在直线为x轴,建立平面直角坐标,且C坐标(8,6),点P在AB上,AP=2,E、F同时从点P出发,分别沿PA、PB以每秒1个单位的速度向A、B匀速运动,点E到达A后立即以原速沿AB向B运动,点E再次返回点P停止,点F也随之停止运动,在点E、F运动过程中,以EF为边向上做正方形EFGH,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
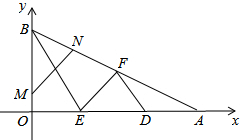 如图,在平面直角坐标系中,Rt△ABO的顶点A、B的坐标分别为(3,0)、(0,1),点D、E是AO的三等分点,且点D在点E的右侧,点F是AB的中点.动点P从点B出发,以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动.当点P不与点E、F重合时,过点P作其运动所在线段的垂线,交AB边于点N,交BO或AO于点M.设点P运动时间为t(秒).
如图,在平面直角坐标系中,Rt△ABO的顶点A、B的坐标分别为(3,0)、(0,1),点D、E是AO的三等分点,且点D在点E的右侧,点F是AB的中点.动点P从点B出发,以每秒$\sqrt{2}$个单位长度的速度沿折线BE-EF-FD运动.当点P不与点E、F重合时,过点P作其运动所在线段的垂线,交AB边于点N,交BO或AO于点M.设点P运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 20吨以下(含20吨) | a | 1.50 |
| 超过20吨但不超过30吨的部分 | b | 1.50 |
| 超过30吨的部分 | 4.50 | 1.50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com